Publication initiale : 4 juillet 2025
À savoir avant de commencer :
Le hachage est une opération qui consiste à convertir dans un bloc de longueur fixe, appelé empreinte, un texte ou message d'une longueur quelconque (en réalité, il y a une limite mais celle-ci est très grande). Le hachage est effectué à l'aide d'un algorithme consacré à cette tâche comme SHA-256, de la famille SHA-2 (SHA pour Secure Hash Algorithm). Celle-ci est très largement utilisée sur Internet et sera décrite plus en détail dans cet article.
|
(Texte brut) bonjour |
| ↓ |
|
2CB4B1431B84EC15D35ED83BB927E27E8967D75F4BCD9CC4B25C8D879AE23E18 (Empreinte avec algorithme de hachage SHA-256, notation hexadécimale) |
L'empreinte fournie par un algorithme de hachage paraît avoir un aspect cryptographique comme montré ci-dessus et peut ressembler à un message secret chiffré par un émetteur et déchiffré par son destinataire, mais ce n'est pas le cas. Le hachage est différent du chiffrement des données et ne doit pas être confondu avec ce dernier.
Le hachage sert d'une certaine manière à protéger des données, au même titre que le chiffrement, mais dans le but d'en vérifier l'intégrité et non pas d'en faire des textes secrets. Le hachage peut permettre aussi d'authentifier des données (plus de détails à ce sujet plus loin dans l'article), ce qui est différent du chiffrement des données.
La conception d'un algorithme de hachage repose notamment sur le principe de fournir un résultat presque unique pour chaque texte brut. Les risques de « collision » résultant d'un hachage, c'est-à-dire la possibilité d'avoir une même empreinte pour deux textes différents fournis en entrée, sont toujours possibles puisqu'un algorithme de hachage peut accepter en principe un nombre extrêmement élevé de textes bruts différents. Dans ce cas, il peut inévitablement se produire en principe des collisions mais les risques demeurent très faibles.
En dépit de l'apparence aléatoire qu'une empreinte de hachage telle que vue dans l'exemple montré plus haut, celle-ci sera toujours la même à chaque fois qu'on lui fournit en entrée le même texte brut. Ainsi, le mot « bonjour » va toujours donner la même empreinte à chaque fois qu'on l'utilise avec l'algorithme SHA-256. Cela fait en sorte que le hachage est un algorithme « déterministe ».
De plus, l'empreinte fournie par un algorithme de hachage est irréversible, c'est-à-dire qu'il n'est pas possible de déterminer le texte initial fourni en entrée à partir de l'empreinte. Ainsi avec l'empreinte donnée en exemple plus haut, on ne peut pas, en faisant le chemin inverse à partir de l'empreinte, savoir qu'elle correspond au mot « bonjour ».
Finalement, un algorithme de hachage va retourner des empreintes très différentes pour deux valeurs en entrée qui sont presque identiques et qui n'ont qu'une très légère différence entre eux. C'est ce qu'on appelle l'« effet avalanche », par analogie au fait qu'une toute petite perturbation dans les hauteurs enneigées d'une montagne peut déclencher une énorme avalanche.
|
(Texte brut de l'exemple montré plus haut mais avec un B majuscule) Bonjour |
| ↓ |
|
9172E8EEC99F144F72ECA9A568759580EDADB2CFD154857F07E657569493BC44 (Empreinte avec algorithme SHA-256) |
Comparaison :
2CB4B1431B84EC15D35ED83BB927E27E8967D75F4BCD9CC4B25C8D879AE23E18 (bonjour)
9172E8EEC99F144F72ECA9A568759580EDADB2CFD154857F07E657569493BC44 (Bonjour)
L'utilisation la plus simple d'un algorithme de hachage consiste à vérifier l'intégrité des données transmises entre un émetteur et un destinataire selon la description donnée en étapes dans les prochaines sections.
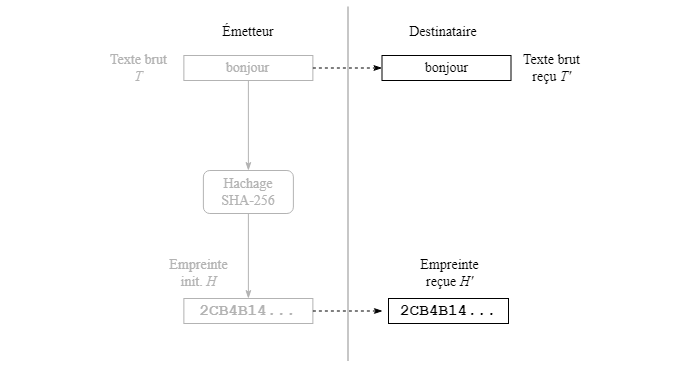
L'émetteur applique l'algorithme de hachage au texte brut T afin d'obtenir l'empreinte initiale H.

L'émetteur transmet le texte brut T et l'empreinte H. Le destinataire reçoit les données (censément les mêmes) qui, de son côté, sont nommées T' et H', respectivement.
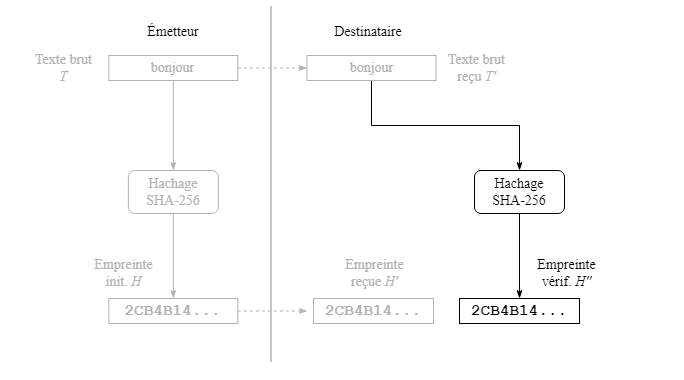
Le destinataire applique l'algorithme de hachage au texte brut reçu T' afin d'obtenir une empreinte de vérification H''.
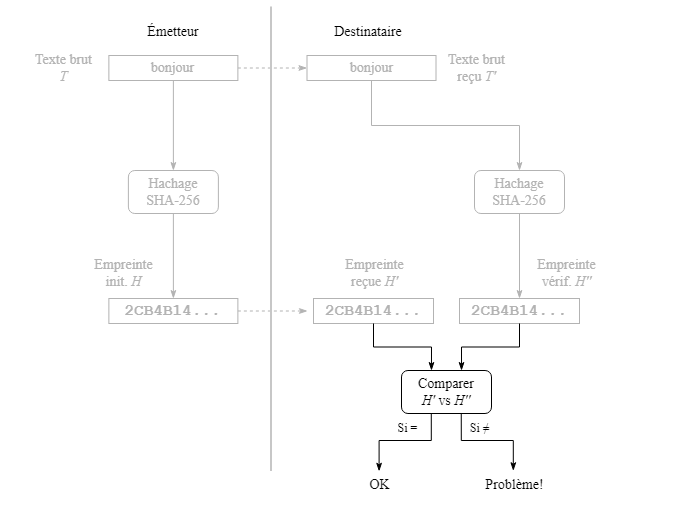
Le destinataire compare l'empreinte reçue H' avec celle de vérification H''. Si les empreintes sont identiques, l'intégrité du texte transmis est assurée. Dans le cas, contraire, les données sont compromises, soit par une manipulation intentionnelle non autorisée, soit suite à un incident quelconque (ex. : difficulté dans la communication).
Si seul le texte brut T est altéré, celui-ci donnera une empreinte de vérification H'' différente de l'empreinte reçue H' (qui n'a pas changé) du côté du destinataire et une erreur sera détectée dans cette situation.
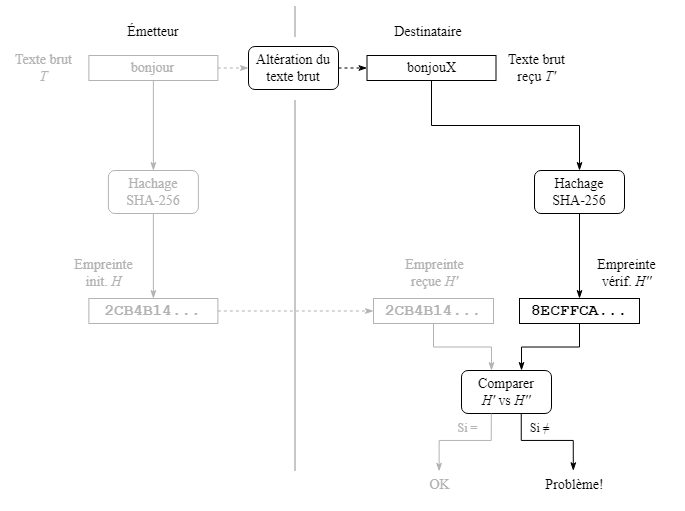
Si seule l'empreinte H est altérée, l'empreinte reçue H' sera différente de l'empreinte initiale et de celle de vérification H'', ce qui sera aussi détecté comme une erreur.
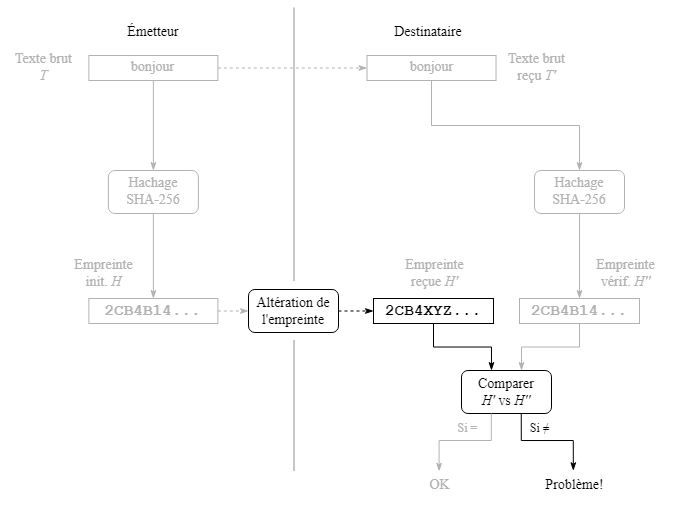
Les cas d'altération du texte brut seul ou de l'empreinte seule présentés précédemment sont plus susceptibles de se produire lors de difficultés techniques dans la communication (ex. : bris, bruit) entre l'émetteur et le destinataire. Cependant en cas d'intervention malveillante par un tiers, il est plus probable que le texte brut ainsi qu'une empreinte tout à fait valide pour ce texte se substituent aux données envoyées par l'émetteur. L'utilisation du hachage en prenant en compte seulement le texte brut n'est pas suffisante pour prevenir un tel cas et un volet authentification est nécessaire pour cela.
Pour prévenir toute manipulation malintentionnée des données entre l'émetteur et le destinataire, une clé commune, connue seulement de l'émetteur et du destinataire, doit alors être ajoutée au texte brut et ainsi être incluse dans l'opération de hachage pour rendre la transmission plus sécuritaire.
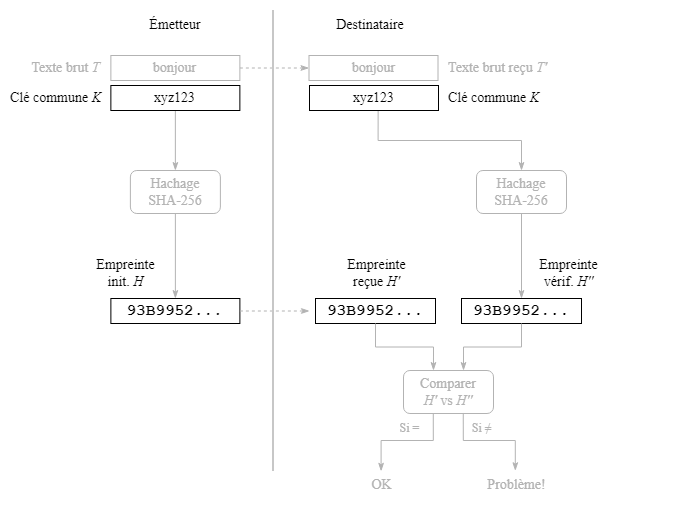
Les algorithmes de hachage sont aussi utilisés pour la gestion des mots de passe des comptes d'utilisateurs pour des sites Internet. Le modèle d'opération pour la gestion des mots de passe est différent de ce qui a été montré précédemment mais celui-ci repose essentiellement sur le principe d'authentification.
Dans ce modèle, tout le travail est fait au niveau de serveur du site. Une gestion rigoureuse et sérieuse des mots de passe par un site exigera de celui-ci de ne jamais conserver sur le serveur les mots de passe en clair. Il doit plutôt conserver leurs empreintes.
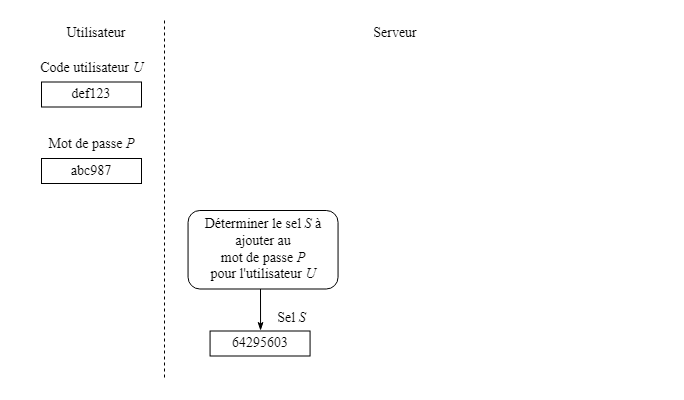
Un des algorithmes les plus utilisés pour la gestion des mots de passe est l'algorithme bcrypt. Celui-ci a recours à un nombre aléatoire, appelé le « sel », généré lors de la création (ou modification) du mot de passe. Ce sel agit à titre de « clé commune connue de l'émetteur et du récepteur » telle que mentionnée à la section précédente concernant le volet authentification.
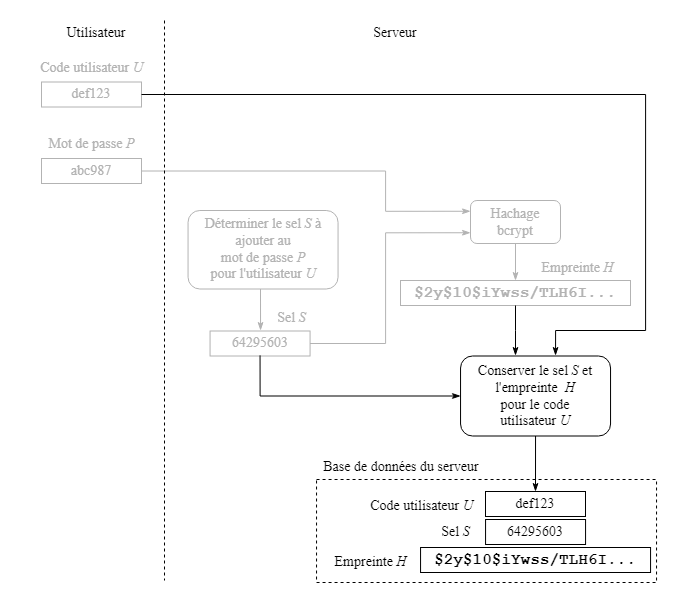
L'utilisateur entre d'abord son code U et le mot de passe de son choix P, puis le serveur détermine le sel S à l'aide d'un générateur de nombres aléatoires.
Le serveur poursuit en appliquant l'algorithme de hachage bcrypt au mot de passe P et au sel S mis bout à bout afin d'obtenir l'empreinte H.
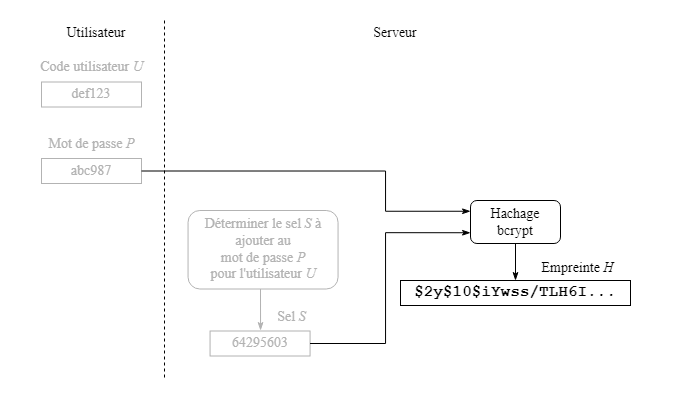
Le code d'utilisateur U, le sel S et l'empreinte H sont finalement conservés dans la base de données du serveur.
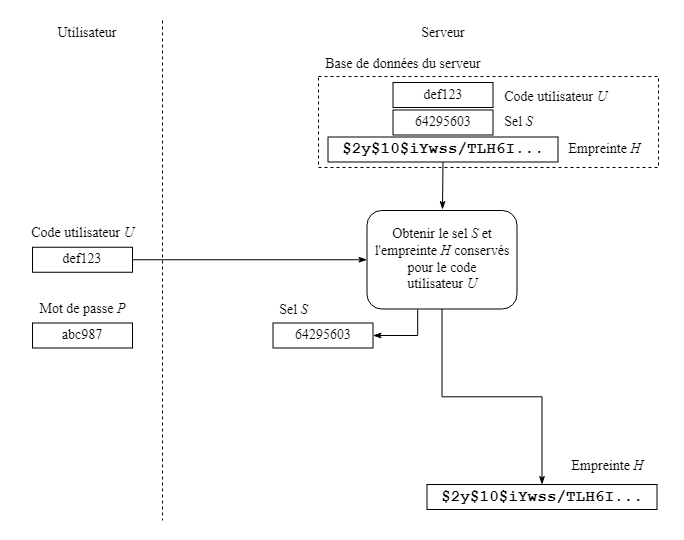
L'utilisateur entre d'abord son code U et le mot de passe P, puis le serveur récupère de sa base de données le sel S et l'empreinte H pour l'utilisateur U.
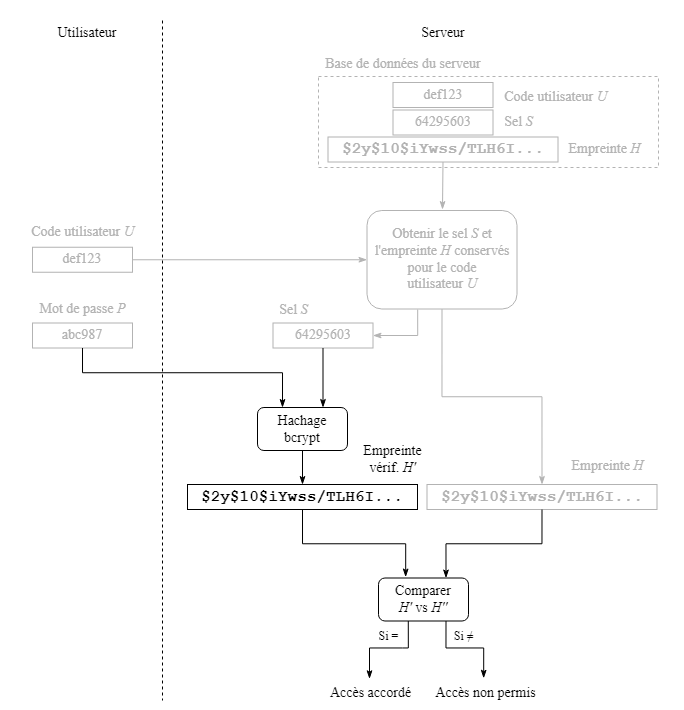
Le serveur valide le mot de passe P entré par l'utilisateur en lui ajoutant le sel S afin d'appliquer au tout l'algorithme bcrypt pour obtenir l'empreinte de vérification H'. Il fait ensuite la comparaison entre cette empreinte et celle déjà conservée, H, afin de déterminer si l'accès doit être accordé ou non à l'utilisateur.
Comme son nom l'indique, la blockchain est séparée en blocs reliés entre eux et chaque nouveau bloc ajouté à la chaîne est le résultat d'une « compétition », appelée le minage, entre des noeuds du réseau. Le « gagnant » reçoit une récompense puisée dans les frais de transactions effectuées dans le réseau de la blockchain.
Dans la blockchain, le hachage est principalement effectué dans les contextes suivants :
Identifier les transactions par des empreintes et valider celles-ci lorsqu'elles sont ajoutées à un bloc;
Relier les blocs entre eux pour rendre impossible toute altération de l'un ou l'autre de ceux-ci par une partie mal intentionnée;
Pour le minage, générer de façon répétitive des empreintes à partir des données des transactions incluses dans un bloc en utilisant à chaque fois un nouveau nombre aléatoire jusqu'à ce qu'un noeud soit désigné le « gagnant » pour la création d'un nouveau bloc dans la blockchain.
Pour les prochaines sections, nous allons utiliser comme modèle d'algorithme de hachage l'algorithme SHA-384, qui utilise une empreinte H de 512 bits. Cet algorithme fait également partie de la famille SHA-2 au même titre que SHA-256, utilisé jusqu'ici dans l'article et basé sur une empreinte de 256 bits.
Bien qu'il soit moins utilisé actuellement sur Internet que SHA-256, l'algorithme SHA-384 est tout de même très répandu dans les organisations (gouvernement, institutions bancaires, etc.) conservant des données sensibles afin d'en accroître le degré de protection avec une plus longue empreinte. Le principe général de fonctionnement est le même pour les deux algorithmes (comme pour toute la famille SHA-2 d'ailleurs); la différence se situe principalement au niveau de la taille des données manipulées, dont l'empreinte.
Le but de l'algorithme SHA-384 est de produire une empreinte très probablement unique de 512 bits H pour un texte brut T d'une longueur quelconque. Le résultat retourné est constitué des 384 premiers bits de l'empreinte H.
Avant de commencer l'exécution de l'algorithme, un prétraitement qui consiste à ajouter certaines données additionnelles de contrôle à la fin du texte brut est effectué afin que le tout consiste en un « texte formaté » Tf dont la longueur est un multiple exact de 1024 bits. Le détail sur les données additionnelles est donné un peu plus loin, à la section 5.1.

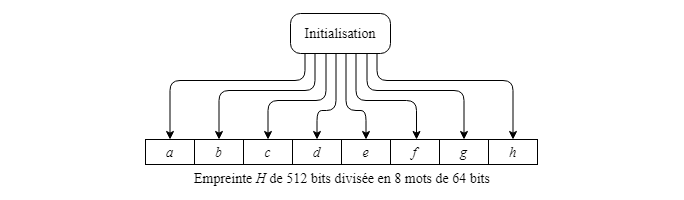
Le début de l'algorithme comprend également une étape d'initialisation de l'empreinte H avec des valeurs prédéfinies. Pour cela, l'empreinte de 512 bits est divisée en 8 mots de 64 bits, identifiés de a à h. Les valeurs, déterminées par les concepteurs de l'algorithme, sont données à l'annexe A.
Une fois le prétraitement et l'initialisation de l'empreinte complétés, le traitement de l'algorithme consiste à diviser conceptuellement le texte formaté Tf en blocs de 1024 bits et à appliquer pour chaque bloc de 1024 bits parcouru une série de transformations de l'empreinte H à partir du contenu du bloc. Le contenu de l'empreinte H après le dernier bloc constitue le résultat fourni en sortie par l'algorithme.
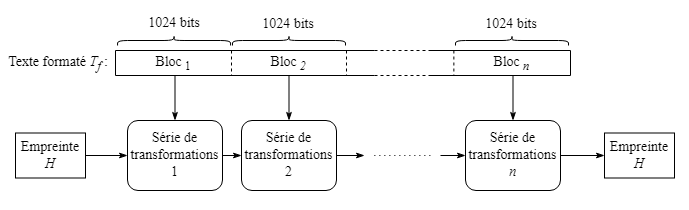
Chaque série de transformations de l'empreinte H pour un bloc donné consiste à appliquer sur l'empreinte 80 rondes de transformation numérotées de 0 à 79. En support aux rondes de transformations, deux tableaux de 80 éléments chacun, K et W, sont utilisés. Les éléments dans chacun de ceux-ci sont également numérotés de 0 à 79 afin qu'ils correspondent chacun à la ronde du même numéro.
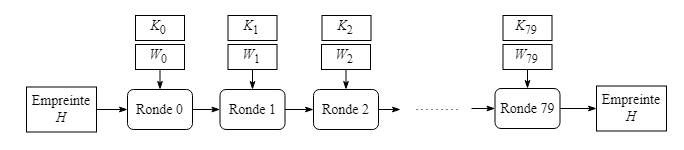
Le premier tableau K contient des constantes dont les valeurs ne changent pas d'un bloc de 1024 bits à l'autre. Les valeurs des constantes sont données à l'annexe B.
Le second tableau, le tableau de contrôle W, a un contenu qui change à chaque bloc de 1024 bits. Pour le mettre à jour, on utilise le bloc actuel de 1024 bits en le divisant en 16 mots de 64 bits. On reproduit ensuite les valeurs de ceux-ci dans les 16 premiers éléments W0 à W15.
Les valeurs dans W0 à W15 sont ensuite utilisées pour propager des nouvelles valeurs aux éléments W16 à W79 qui sont modifiées d'un élément à l'autre. Le procédé utilisé à cette fin est donné en détail un peu plus loin, à la section 5.2.

Cette section donne de manière plus formelle des détails sur les parties les plus complexes de l'algorithme dont la description générale a été présentée à la section précédente. Il est important ici d'avoir certaines connaissances concernant les opérations modulo et les opérations sur des bits comme le OU exclusif et le décalage pour avoir une certaine compréhension du contenu de la section. Les lecteurs moins familiers peuvent tout de même se baser sur les sections précédentes pour avoir un aperçu général du fonctionnement d'un algorithme de hachage et passer immédiatement à la prochaine section 6 (Autres algorithmes de la famille SHA-2).
Comme mentionné plus tôt à la section 4.1, un prétraitement consistant à ajouter certaines données additionnelles à la fin du texte brut T est effectué. Ces données sont indiquées ci-dessous :
Tout l'ensemble composé du texte brut T et des données additionnelles mentionnées ci-dessus formera le texte formaté Tf servant à l'opération de hachage dans son entier afin de transformer l'empreinte H. L'ajout des données additionnelles fait en sorte que la longueur de Tf sera toujours un multiple de 1024 bits.
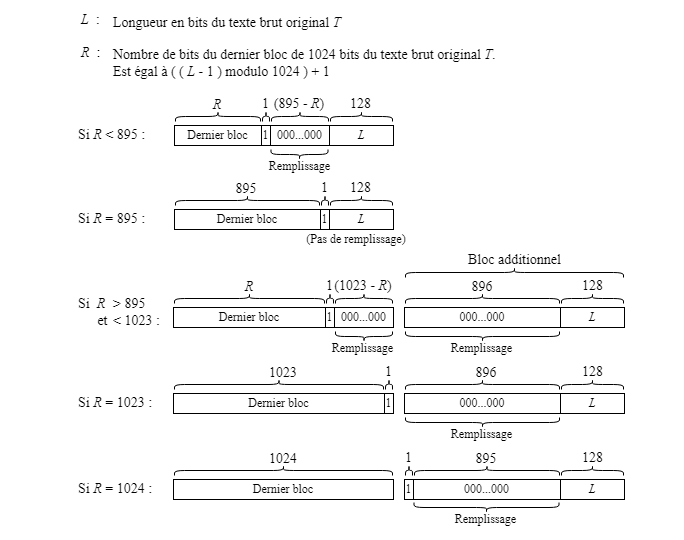
Dans certains cas, l'ajout des données additionnelles peut nécessiter l'ajout d'un bloc de 1024 bits additionnel. Le tout dépend du nombre de bits R dans le dernier bloc de 1024 bits du texte brut original T. Les différentes possibilités concernant la manière de disposer les données additionnelles sont montrées ci-dessous.
Comme mentionné plus tôt à la section 4.4.2, les 16 premiers éléments de W contiennent essentiellement les mêmes valeurs que celles des 16 mots de 64 bits formant le bloc de 1024 bits où l'on est rendu.
Pour les éléments aux positions 16 à 79 du tableau W, le traitement est plus complexe comme en fait foi le diagramme ci-dessous.
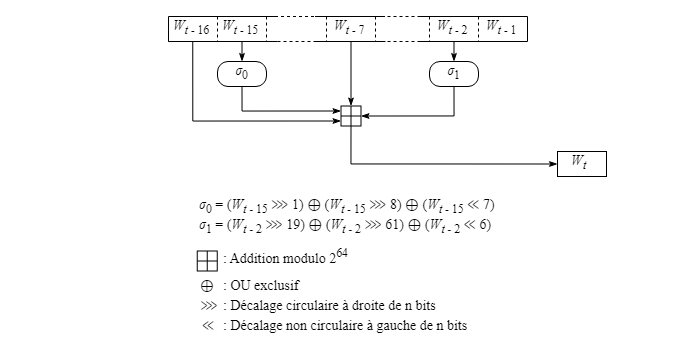
Les symboles σ0 et σ1 utilisés dans la figure ci-dessus sont ceux mentionnés tels quels par les concepteurs de l'algorithme.
Pour chaque élément à la position t dans le tableau, il faut ainsi prendre en compte les valeurs des éléments aux positions suivantes : t - 2, t - 7, t - 15 et t - 16.
Exemples :
L'addition modulo 264 mentionnée dans le diagramme est utilisée à plusieurs reprises dans l'algorithme. Cette addition se fait entre deux mots de 64 bits et consiste à ne garder que les 64 bits les moins significatifs du résultat de l'addition.
L'exemple simplifié ci-dessous en base 28 permet d'illustrer l'opération. Le principe est essentiellement le même avec la base 264 car il s'applique de façon identique à toutes les puissances de 2.
| Binaire | Hexa | Décimal | ||||||
|---|---|---|---|---|---|---|---|---|
| 10011101 | 9D | 157 | ||||||
| + | 10101010 | + | AA | + | 170 | |||
| = | 101000111 | = | 147 | = | 327 | |||
| = 01000111 | (mod 28) | = 47 | (mod 100 [hexa]) | = 71 | (mod 256) |
La « perte » de bits découlant de l'addition modulo constitue en fait un avantage pour l'algorithme de hachage car elle lui permet d'être irréversible, faisant en sorte qu'il n'est pas possible de reconstituer le texte brut original à partir de l'empreinte résultant de l'algorithme.
Cette partie constitue le noyau de l'algorithme SHA-384. Sa fonction est, lors de toute ronde de transformation pour un bloc de 1024 bits donné, d'attribuer aux mots a à h de l'empreinte H des nouvelles valeurs correspondantes a' à h' et par le fait même un nouveau contenu d'empreinte H'. Pour cela, plusieurs opérations sur des bits choisies par les concepteurs de l'algorithme sont utilisées.
La partie la plus simple d'une ronde de transformation consiste à déterminer les nouvelles valeurs pour b', c', d', f' g' et h'. La même opération est employée pour chacun de ces mots et consiste à faire l'addition modulo 264 de l'ancienne valeur du mot et celle du mot qui précède dans l'empreinte.
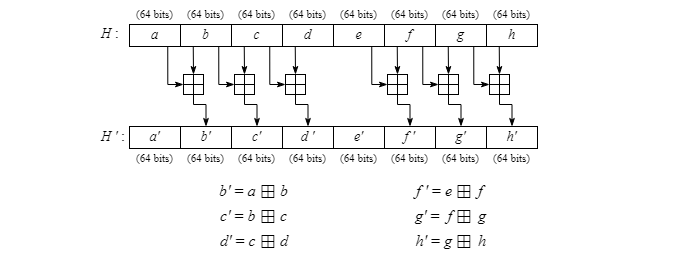
Pour déterminer la nouvelle valeur a', les calculs sont nettement plus complexes tels que montrés ci-dessous.
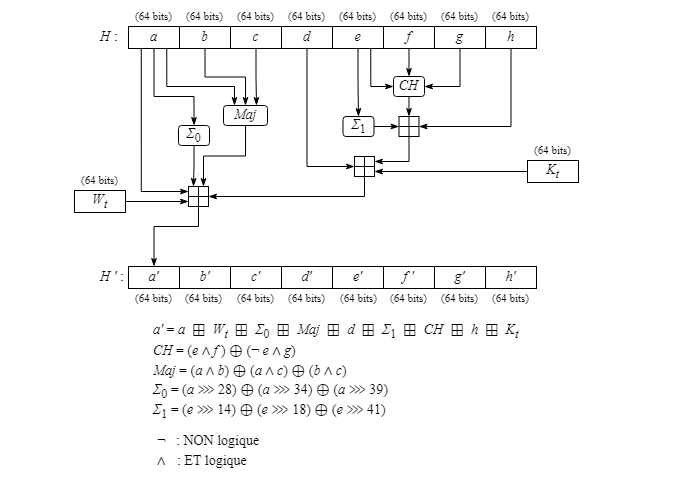
Sans entrer dans les détails, les calculs pour la nouvelle valeur de a utilisent essentiellement toutes les anciennes valeurs de a à h. Le mot de contrôle Wt et la constante Kt correspondant à la ronde sont également employés. Les symboles Σ0, Σ1, CH et Maj sont ceux utilisés par les concepteurs de l'algorithme.
Pour déterminer la nouvelle valeur e', il y a moins de calculs mais ceux-ci demeurent complexes.
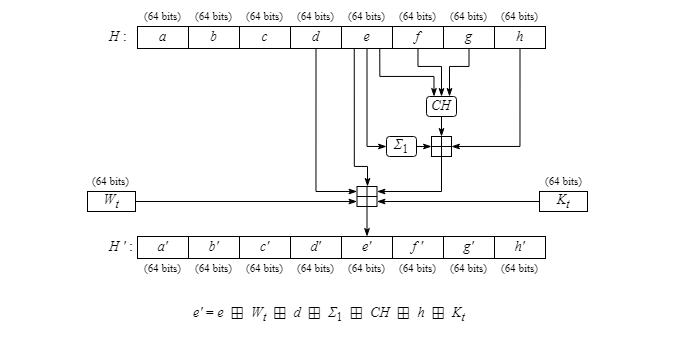
Le tableau ci-dessous donne la liste des algorithmes de la famille SHA‑2 et les principales différences entre eux.
| Algorithme | Taille mot (octets / bits) | Longueur H (bits) | Longueur bloc (bits) | Partie de H retenue | Rondes transf. | Long. max. texte (bits) |
|---|---|---|---|---|---|---|
| SHA-224 | 4 / 32 | 256 | 512 |
a b c d e f g (224 bits) |
64 | 264 |
| SHA-256 | 4 / 32 | 256 | 512 |
a b c d e f g h (256 bits) |
64 | 264 |
| SHA-384 | 8 / 64 | 512 | 1024 |
a b c d e f g (384 bits) |
80 | 2128 |
| SHA-512 | 8 / 64 | 512 | 1024 |
a b c d e f g h (512 bits) |
80 | 2128 |
| SHA‑512/224 | 8 / 64 | 512 | 1024 |
a b c d * (224 bits) |
80 | 2128 |
| SHA‑512/256 | 8 / 64 | 512 | 1024 |
a b c d (256 bits) |
80 | 2128 |
Comme mentionné plus tôt au début de la section 4, l'algorithme SHA‑384 utilise une empreinte H de 512 bits et des blocs de 1024 bits de texte formaté basés sur des mots de 64 bits. Ce n'est cependant pas le cas de tous les algorithmes de la famille SHA‑2 dont SHA‑384 fait partie.
Les algorithmes SHA‑224 et SHA‑256, de leur côté, utilisent des mots de 32 bits, ce qui se répercute dans la longueur de l'empreinte H — qui comprend 8 mots pour toute la famille SHA‑2 — ainsi que dans la longueur du bloc utilisée pour diviser un texte formaté (le bloc comporte toujours 16 mots). SHA‑224 et SHA‑256 utilisent par ailleurs moins de rondes de transformation.
Les algorithmes ont également des différences entre eux concernant les points suivants, non indiqués dans le tableau :
Bien que les algorithmes de hachage ne soient pas utilisés pour faire du chiffrement de données, les empreintes qui sont conservées suite à leur application recèlent souvent des données sensibles (mot de passe, numéro de carte de crédit, etc.) et peuvent ainsi être des cibles d'attaques numériques.
Étant donné le caractère irréversible des empreintes de hachage, il n'est pas possible de reconstituer à partir d'une empreinte le texte brut qui en est à l'origine. Le travail à effectuer pour une intervention malveillante consiste donc plutôt à prendre un texte brut quelconque et tenter de générer une empreinte identique à une autre qui est déjà conservée sur un serveur.
Les algorithmes de hachage couramment utilisés comme SHA‑256, SHA‑384 et bcrypt constituent des valeurs sûres en matière de sécurité des données. L'empreinte de 256 bits de SHA‑256 et celle de 384 bits pour SHA‑384 sont suffisamment grandes pour rendre impossible la tâche de générer des empreintes identiques dans le cadre d'une attaque par force brute.
Du côté de l'algorithme bcrypt, l'empreinte est de 192 bits. Bien que cette empreinte soit plus petite, l'application de l'algorithme bcrypt est beaucoup plus lente que celle de SHA‑256 et SHA‑384, ce qui rend également très compliquée la possibilité de faire une attaque par force brute.
Avec l'émergence des ordinateurs quantiques dans un futur plus ou moins lointain, les algorithmes comme SHA‑256, SHA‑384 et bcrypt devraient demeurer des moyens fiables pour protéger les données. Ceux-ci peuvent résister à l'application de l'algorithme de Grover, un algorithme développé pour les ordinateurs quantiques permettant de réduire de la racine carrée l'effort actuellement requis pour une attaque par force brute.
Considérant que l'effort d'une attaque par force brute pour SHA‑256, par exemple, est de l'ordre de 2256 (environ 1077) opérations, cela donnerait 2128 (environ 1038) opérations à effectuer, ce qui est encore énorme, même pour un ordinateur quantique. L'utilisation de SHA‑384 augmente exponentiellement cet ordre de complexité.
Pour l'algorithme bcrypt, le principe est similaire, en réduisant de moitié l'exposant. De 2192 (environ 1057) opérations requises, on passe à 296 (environ 1028) opérations pour une attaque par force brute avec l'algorithme de Grover. En prenant en compte la lenteur de l'application de l'algorithme bcrypt, l'opération demeure impensable.
Malgré les signes rassurants concernant les algorithmes de hachage, une certaine vigilance est de rigueur car d'autres algorithmes plus performants que Grover pourraient voir le jour et compromettre leur sécurité. C'est pourquoi des recherches sont en cours pour trouver des alternatives « post-quantiques » aux algorithmes existants, même si ceux-ci sont robustes.
De façon sommaire, un algorithme de hachage permet d'obtenir une empreinte numérique quasi-unique pour un texte brut. Grâce à l'effet avalanche, cette empreinte sera très différente si on modifie le moindrement le texte brut. Par exemple, « bonjour » et « Bonjour » vont générer des empreintes complètement différentes qui ne permettront pas de voir que la seule différence entre les deux mots est le « B » majuscule au début.
La faculté d'un algorithme de hachage de produire une empreinte irréversible procure un certain degré de confidentialité dans le sens qu'il n'est pas possible de reconstituer le texte brut à partir de l'empreinte. Ce n'est toutefois pas le seul facteur qui contribue à rendre un algorithme de hachage robuste sur le plan sécuritaire; la taille de l'empreinte et la lenteur de l'algorithme y sont pour beaucoup.
L'utilisation à laquelle est destinée l'empreinte résultant d'un hachage consiste à comparer cette empreinte avec une autre empreinte afin de vérifier si les deux empreintes ont été déterminées pour le même texte brut. Un résultat indiquant que les deux empreintes sont pareilles permet d'assurer l'intégrité des données ou, selon le cas, d'authentifier un accès quelconque.
Constantin, L. (2021, 13 janvier). Hashing explained: Why it’s your best bet to protect stored passwords. CSO.
Bybit (2023, 7 novembre). Explained: What Is Hashing in Blockchain?. Bybit.
Les mots de 64 bits a à h composant l'empreinte H de bits sont initialisés avec les valeurs suivantes, déterminées par les concepteurs de l'algorithme :
Remarques :
(Notation hexadécimale)
Remarque :