Corps finis et chiffrement des données

Publication initiale : 4 juillet 2025

1. Introduction

La théorie des corps finis a été développée au début du XIX^e siècle par le jeune mathématicien Évariste Galois, mort à seulement 20 ans. Elle est notamment utilisée en cryptographie informatique où elle joue un rôle fondamental. Certains principes généraux de cette théorie seront décrits de manière plus ou moins formelle dans cet article. L'accent sera davantage mis, avec des exemples, sur leur application dans le domaine du chiffrement des données et en particulier l'algorithme AES-256.

2. Description sommaire

Un corps fini est un ensemble contenant un nombre fini d’éléments (appelé son cardinal) dans lequel on peut effectuer les opérations d’addition, de soustraction, de multiplication et de division (sauf par zéro), avec les mêmes règles que dans les nombres usuels. On peut noter les propriétés suivantes d'un corps fini :

• Le cardinal d'un corps fini est toujours une puissance d'un nombre premier p, soit pⁿ;
• p est un nombre premier appelé la caractéristique du corps;
• n est un nombre entier positif appelé le degré d'extension du corps fini.

2.1 Notations employées

Un corps fini peut être noté comme suit :

F_q (où q = pⁿ)

La notation suivante peut aussi être employée si q donne un nombre trop grand :

F_pn

Dans la documentation anglo-saxonne sur le sujet, on retrouve souvent la notation suivante :

GF(q) ou encore GF(pⁿ) {GF pour Galois Field}

2.2 Cas particulier des corps de caractéristique 2

Les corps finis de caractéristique 2 se prêtent très bien au traitement en mode binaire par ordinateur en raison de l'utilisation de la base 2 et l'attention principale du présent article sera portée sur ceux-ci.

3. Représentation polynômiale

Les éléments d'un corps fini sont souvent représentés de manière formelle par des polynômes de degré inférieur au degré d'extension n du corps fini sous la forme suivante :

c_{n - 1} x^{n - 1}  +  c_{n - 2} x^{n - 2}  +  . . .  +  c₁ x¹  +  c₀ x⁰

Chaque coefficient c_i doit être une valeur entière comprise entre 0 et p - 1.

3.1 Adaptation en représentation binaire

Pour un corps de caractéristique p = 2, ce formalisme peut être ramené à une représentation binaire plus familière en dépit de l'utilisation du terme « polynôme ». Prenons par exemple un polynôme avec un degré d'extension n = 8. Celui-ci sera exprimé comme suit :

c₇ x⁷  +  c₆ x⁶  +  c₅ x⁵  +  c₄ x⁴  +  c₃ x³  +  c₂ x²  +  c₁ x¹  +  c₀ x⁰

Pour avoir une représentation binaire, on enlève tous les termes en x et les opérateurs + dans le polynôme :

c₇    c₆    c₅    c₄    c₃    c₂    c₁    c₀

Comme mentionné plus haut, les coefficients c_i sont des entiers compris entre 0 et p - 1. Étant donné que p ici est égal à 2, les coefficients ne peuvent donc avoir que la valeur 0 ou 1, ce qui correspond à des bits d'une représentation binaire d'un nombre.

Voyons maintenant avec un exemple dans le corps fini F₂₅₆ :

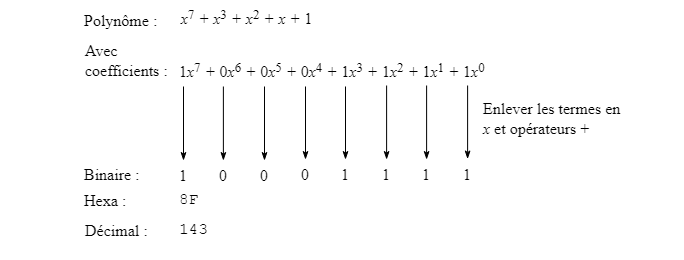
Avec cet exemple on peut faire les constatations suivantes :

• L'exposant de chaque terme du polynôme correspond à la position d'un bit en représentation binaire;
• Le coefficient de chaque terme dans le polynôme correspond à la valeur du bit à la position selon l'exposant.

En étendant le principe pour l'ensemble du corps fini F₂₅₆ qui comporte 256 éléments, on obtient un domaine composé des valeurs binaires de 00000000 à 11111111.

4. Addition et soustraction

4.1 Addition et soustraction en représentation polynômiale

L'addition et la soustraction selon la représentation polynômiale d'un corps fini de caractéristique p commencent de la même manière que celle employée pour les polynômes conventionnels. Voyons avec un exemple d'addition :

Pour débuter, on fait le regroupement des termes des polynômes selon les exposants :

On additionne ensuite les coefficients pour chaque groupe selon l'exposant :

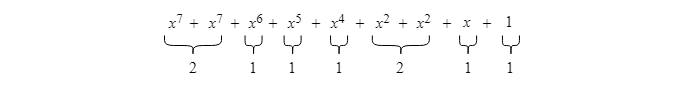
À ce point-ci, l'addition et la soustraction de polynômes dans un corps fini diffèrent de celles pour les polynômes conventionnels. Lorsque les opérations sont effectuées dans un corps fini, il faut appliquer aux totaux des coefficients la réduction modulo selon la caractéristique p du corps. Si on prend la caractéristique 2 dans l'exemple, on utilise alors la réduction modulo 2 :

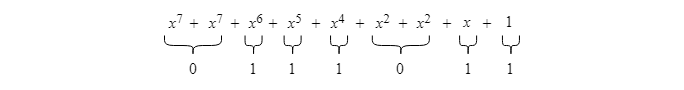
En récrivant le polynôme avec les nouveaux coefficients, on obtient le résultat de l'addition dans un corps fini :

4.2 Addition et soustraction en représentation binaire

Lorsqu qu'on fait l'addition ou la soustraction dans un corps fini de caractéristique 2 en utilisant la représentation binaire, ces opérations sont équivalentes. On utilise alors simplement l'opération de OU exclusif entre les opérandes. On peut voir ci-dessous l'addition en représentation binaire avec le même exemple utilisé jusqu'ici sous forme de polynômes :

5. Polynôme irréductible

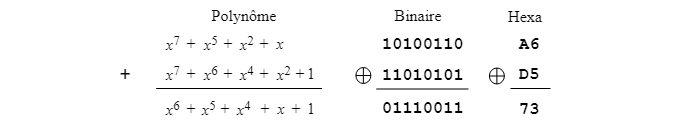
Dans un corps fini F_pn, la multiplication et les autres opérations qui en sont dérivées (inverse multiplicatif et division) nécessitent l'emploi d'un « polynôme irréductible » prédéfini. Celui-ci consiste en un polynôme de degré n qu'il n'est pas possible d'exprimer comme un produit de deux autres polynômes dans le corps fini, c'est pour cette raison qu'on dit que le polynôme est irréductible.

Le polynôme irréductible joue le même rôle dans un corps fini qu'un nombre premier parmi les nombres entiers. Il sert pour la multiplication de polynômes au même titre que le nombre premier dans une mulun nombre composétiplication afin d'obtenir un nombre composé.

Pour un corps fini donné, incluant F₂₅₆, il est possible d'avoir plusieurs polynômes irréductibles. Pour l'algorithme AES-256, par exemple, qui utilise F₂₅₆, le polynôme irréductible choisi est le suivant :

x⁸ + x⁴ + x³ + x + 1 (équivalent en mode binaire : 100011011, ou 11B en mode hexadécimal).

6. Multiplication dans un corps fini

Pour décrire la multiplication P ∙ Q entre deux polynômes dans un corps fini F_pn, nous allons examiner l'opération dans le contexte des corps finis de caractéristique 2 puisque l'article porte principalement l'attention sur ceux-ci.

La multiplication dans un corps fini se fait en deux grandes étapes :

• Multiplication brute;
• Réduction modulo selon le polynôme irréductible.

Nous allons voir plus en détail chacune de celles-ci dans les prochaines sections avec un exemple dans le corps fini F₂₅₆ (donc de caractéristique p = 2 et de degré d'extension n = 8), avec le polynôme irréductible utilisé pour l'algorithme AES-256 : x⁸ + x⁴ + x³ + x + 1 (binaire : 100011011, hexadécimal : 11B).

À noter que le polynôme irréductible n'est pas utilisé pour l'étape de multiplication brute et est réservé pour celle de réduction modulo.

6.1 Première étape : multiplication brute

Cette étape sera décrite en employant la représentation polynômiale, qui est plus compliquée mais qui se rapproche plus du concept général, et la représentation binaire, plus simple mais applicable seulement aux corps finis de caractéristique 2.

6.1 1 Multiplication brute en représentation polynômiale

À titre d'exemple, prenons la multiplication à faire entre les polynômes P (multiplicande) et Q (multiplicateur) suivants :

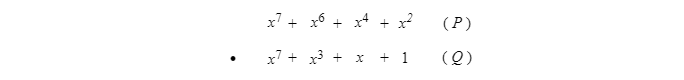
La première chose à faire est de faire correspondre en paires chaque terme d'un des polynômes à chacun des termes de l'autre polynôme et à multiplier les termes de chaque paire :

Les résultats obtenus consistent en eux-mêmes des polynômes. On additionne ensuite chacun de ces polynômes selon la même méthode que celle exposée à la section 4. Pour cela, on fait le regroupement des termes selon les exposants :

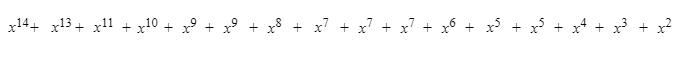
On additionne les coefficients pour chaque groupe selon l'exposant :

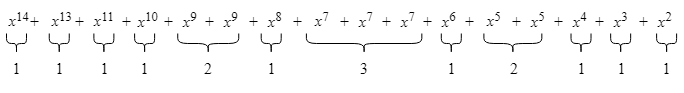
Et on applique la réduction modulo 2 à chaque total de coefficients :

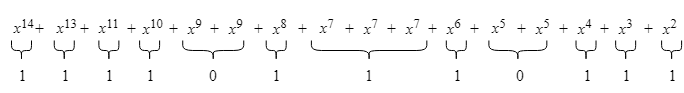
En récrivant le polynôme avec les nouveaux coefficients, on obtient le résultat de la multiplication brute :

La valeur binaire équivalant au résultat de la multiplication brute est 110110111011100.

6.1 2 Multiplication brute en représentation binaire

Faisons la même démarche, en employant cette fois-ci la représentation binaire. Pour cela, employons la méthode suivante pour les polynômes P (multiplicande) et Q (multiplicateur) :

• Utiliser les positions des bits du mutliplicateur Q qui ont la valeur 1;
• Pour chacun de ces bits du multiplicateur Q, en partant du plus significatif, on décale vers la gauche la valeur du multiplicande P autant de fois selon la position du bit, en complétant par des 0 par la droite;
• Additionner toutes les valeurs décalées avec un OU exclusif.

Le développement pour obtenir le résultat de la multiplication brute suivant cette méthode est montré ci-dessous.

On peut constater que le résultat de la multiplication brute obtenu ici avec la représentation binaire est le même que celui obtenu avec la représentation polynômiale.

6.2 Deuxième étape : réduction modulo selon le polynôme irréductible

Pour cette étape, nous allons strictement utiliser la représentation binaire. Comme on peut le constater, le résultat de la multiplication brute obtenu avec l'exemple, 110110111011100, est passablement long.

Plus particulièrement il excède la valeur maximale du corps fini F₂₅₆ (11111111 en mode binaire) utilisé pour l'exemple et il doit donc être ramené à l'intérieur des limites du corps fini. C'est ici que la réduction modulo selon le polynôme irréductible entre en jeu.

Pour cela, nous allons nous inspirer de la division à crochet en appliquant la méthodologie suivante :

• Utiliser le résultat de la multiplication brute comme dividende et comme premier résultat intermédiare;
• Utiliser le polynôme irréductible comme diviseur;
• Pour chaque calcul de nouveau résultat intermédiaire, décaler le polynôme irréductible vers la gauche, en le complétant pas la droite par des 0, jusqu'au bit le plus significatif du dernier résultat intermédiaire;
• Appliquer l'opération de OU exclusif entre le polynôme irréductible décalé et le dernier résultat intermédiaire;
• Appliquer le procédé tant que le résultat intermédiaire n'est pas à l'intérieur du corps fini.

Suivant cette méthodologie, le développement de la réduction modulo selon le polynôme irréductible pour le résultat de la multiplication brute en exemple est présenté ci-dessous.

Le dernier résultat intermédiaire, qui est à l'intérieur des limites du corps fini, constitue le resultat de la multiplication dans le corps fini.

6.3 Bijection de la multiplication dans un corps fini

Le tableau ci-dessous, applicable à l'exemple de multiplication dans un corps fini que nous venons de voir, montre les différents résultats de multiplications pour dans F₂₅₆ avec le polynôme irréductible 100011011 (binaire) qu'il est possible d'avoir en utilisant D4 (hexadécimal) comme multiplicande. Les rangées représentent les 4 bits les plus significatifs du multiplicateur alors que les colonnes désignent les 4 bits les moins significatifs. Suivant ce principe, on retrouve bel et bien la valeur A4 comme résultat pour le multiplicateur 8B de l'exemple.

La présentation du tableau nous permet de faire les constatations suivantes  :

• Toutes les valeurs dans F₂₅₆ apparaissent comme multiplicateurs possibles pour D4;
• Si on observe bien attentivement, toutes les valeurs dans F₂₅₆ apparaissent également comme résultats possibles pour D4;
• Chaque résultat n'apparaît qu'une seule fois que pour un seul multiplicateur;
• Par la nature même du tableau, il n'y a qu'un seul résultat par multiplicateur.

En empruntant un terme issu de la théorie des ensembles, toutes ces propriétés font que la multiplication selon le tableau consiste en une bijection qui peut être illustrée par des correspondances comme suit.

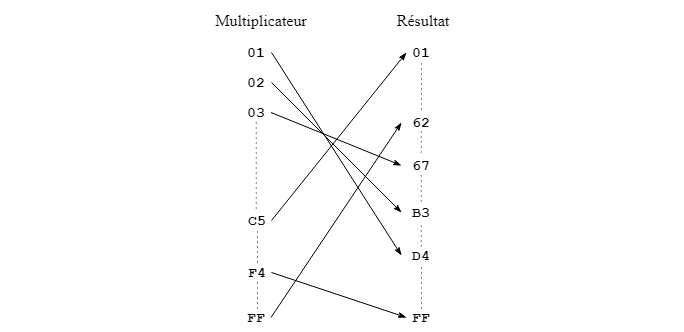
Au-delà de l'exemple montré ici, la nature bijective de la multiplication dans un corps fini s'applique de façon générale à tous les corps finis, pour les valeurs non nulles (i.e. différentes de 0).

6.4 Non-linéarité du produit

Une autre caractéristique de la multiplication dans un corps fini est que le résultat varie énormément sans qu'on puisse établir de lien avec la manière dont varie le multiplicateur, même si ce n'est que très légèrement. Cela fait en sorte que le résultat est « non linéaire » par rapport au multiplicateur et lui donne une apparence imprévisible en passant d'un multiplicateur à l'autre.

En reprenant la rangée pour les multiplicateurs commençant par 0 du tableau de multiplication dans F₂₅₆ pour D4 montré précédemment, on peut constater le caractère quasi-aléatoire des résultats.

Toujours avec l'exemple de la multiplication dans F₂₅₆ pour D4, le graphique de distribution montré ci-dessous permet de représenter visuellement la difficulté d'établir un lien entre le résultat et le multiplicateur.

Par sa capacité de produire des résultats presque imprévisibles, la multiplication dans un corps fini constitue la pierre angulaire dans le domaine du chiffrement des données, notamment avec l'algorithme AES-256. La non-linéarité des résultats permet de « brouiller les cartes » afin que des données secrètes puissent être échangées entre deux parties dans un format incompréhensible pour des observateurs indiscrets.

Outre le corps fini F₂₅₆, l'algorithme AES-256 utilise aussi, lorsqu'il est employé avec le mode GCM (ce qui est la norme dans les échanges sur Internet), le corps F₂128 afin d'augmenter exponentiellement l'apparence de caractère imprévisible de l'opération de multiplication dans un corps fini. L'utilisation de ce corps par AES-256 est accompagnée du polynôme irréductible suivant :

x¹²⁸ + x⁷ + x² + x + 1 (hexadécimal : 1 00000000 00000000 00000000 00000087)

7. Inverse multiplicatif

Pour un élément donné a d'un corps fini F_pn, son inverse multiplicatif est l'élément pour lequel le résultat de la multiplication de a avec celui-ci donne 1 (en employant le polyôme irréductible approprié).

En utilisant comme exemple le corps fini F₂₅₆, une manière de déterminer l'imverse multiplicatif consiste à élever a à la puissance 254 pour obtenir directement le résultat voulu. Cela se fait en un nombre réduit d'étapes par un jeu de multiplications (modulo un polynôme irréductible) en reprenant le résultat de l'étape précédente comme indiqué ci-dessous.

• a³ = a ∙ a ∙ a;
• a⁷ = a³ ∙ a³ ∙ a;
• a¹⁵ = a⁷ ∙ a⁷ ∙ a;
• a³¹ = a¹⁵ ∙ a¹⁵ ∙ a;
• a⁶³ = a³¹ ∙ a³¹ ∙ a;
• a¹²⁷ = a⁶³ ∙ a⁶³ ∙ a;
• a²⁵⁴ = a¹²⁷ ∙ a¹²⁷.

7.1 Pourquoi la puissance 254?

Celle-ci tire son origine d'une des propriétés de l'ensemble des éléments non nuls d'un corps fini de former un « groupe multiplicatif cyclique ». Sans entrer dans les détails qui nous mèneraient un peu loin du cadre de cet article, cela permet de faire l'énoncé suivant pour le corps fini F₂₅₆ pour tout entier non nul a appartenant au corps fini.

a²⁵⁵ ≡ a⁰ (mod 256) {≡ : symbole de congruence qui signifie « est égal à, modulo une certaine valeur »}

Étant donné que tout nombre élevé à la puissance 0 donne comme résultat 1, on peut appliquer ce principe à l'énoncé, qui fait en sorte que a²⁵⁵ est lui aussi égal à 1 :

a²⁵⁵ ≡ a⁰ (mod 256) = 1

Mais a²⁵⁵ est aussi égal à a²⁵⁴ ∙ a. On a donc :

a²⁵⁵ = a²⁵⁴ ∙ a = 1

Cela donne exactement ce que l'on cherche : la valeur a²⁵⁴ à multiplier à a pour avoir 1 comme résultat. Donc, a²⁵⁴ est l'inverse multiplicatif de a dans F₂₅₆, et ce, peu importe le polynôme irréductible employé.

Il existe plusieurs autres méthodes, non montrées dans la présente section, pour déterminer l'inverse multiplicatif mais celle utilisant les multiplications successives donnée plus haut demeure simple et est relativement peu coûteuse en temps d'exécution.

Le tableau ci-dessous utilisé par l'algorithme AES-256 montre en notation hexadécimale tous les inverses multiplicatifs dans F₂₅₆ selon le polynôme irréductible 100011011 (binaire). Les rangées représentent les 4 bits les plus significatifs du nombre dont on veut déterminer l'inverse multiplicatif alors que les colonnes désignent les 4 bits les moins significatifs. Suivant ce principe, on retrouve, par exemple, la valeur EF comme inverse multiplicatif pour B3.

8. Division dans un corps fini

Contrairement à la multiplication dans un corps fini, la division dans un corps fini est très peu utilisée dans les algorithmes de chiffrement.

Quoi qu'il en soit, la division d'un polynôme P par un polynôme diviseur Q dans un corps fini se fait en utilisant des concepts qui ont été montrés dans les sections précédentes, soit en multipliant P par l'inverse multiplicatif de Q.

9. Conclusion

Un corps fini ne s'applique qu'à un nombre premier positif, appelé la caractéristique du corps fini, ou à celui-ci élevé à une certaine puissance exprimée en un nombre entier plus grand que 0, appelée le degré d'extension du corps fini.

Les opérations usuelles d'addition, de soustraction, de multiplication et de division (sauf par 0) s'appliquent à un corps fini.

La multiplication dans un corps fini nécessite l'usage d'un polynôme irréductible. La règle est la même pour opérations de division et d'inverse multiplicatif dans un corps fini, qui sont basées sur la multiplication dans un corps fini.

La représentation polynômiale, qui est fréquemment utilisée pour les corps finis en général, est certes intimidante. Toutefois, lorsqu'il s'agit d'utiliser certains éléments de la théorie des corps finis pour le cas particulier des corps de caractéristique 2, qui sont utilisés pour le chiffrement des données, on peut utiliser à la place la notation binaire, qui est plus familière.

La multiplication et l'inverse multiplicatif dans un corps fini de caractéristique 2 sont les principales opérations utilisées pour le chiffrement des données. Étant par leur nature des bijections. Ces opérations ont le potentiel de produire le plus large éventail possible de résultats avec toutes les valeurs faisant partie du corps fini. Cette faculté et celle de produire des résultats quasi-imprévisibles (non-linéarité) constituent des atouts indispensables pour les algorithmes de chiffrement des données.

Références

Pages Wikipédia