Algorithme AES-256

Publication initiale : 4 juillet 2025

1. Introduction

L'algorithme AES‑256 (AES pour Advanced Encryption Standard) est utilisé pour le chiffrement de données secrètes transmises d'un émetteur à un destinataire sous forme de texte chiffré basé sur l'utilisation d'une clé symétrique de chiffrement déjà connue à l'avance des deux parties. L'algorithme, développé au début des années 2000 par les cryptographes belges Joan Daemen et Vincent Rijmen, est aussi connu sous le nom de Rijndael, résultat de la contraction du nom de ses deux créateurs.

L'utilisation d'une clé de chiffrement par l'algorithme fait en sorte qu'il est impossible reconstituer le texte secret original en partant du texte chiffré si on ne connaît pas la clé.

L'algorithme AES‑256 fait partie de la famille AES qui comprend aussi les algorithmes AES‑128 et AES‑192. Le mode de fonctionnement de ceux-ci est le même que AES‑256, mais avec certaines valeurs différentes de paramètres, notamment la longueur de la clé. Les algorithmes AES‑128 et AES‑192 seront mentionnés plus loin à quelques reprises mais la majeure partie de l'article portera sur AES‑256.

Voyons un exemple de chiffrement avec l'algorithme AES‑256 à l'aide du texte « Bonjour tous les amis! ». Avant de l'aborder, prendre note que la notation hexadécimale y est très utilisée de manière à mieux représenter le traitement fait par l'algorithme, qui fonctionne par octets et par bits. À noter aussi que le texte chiffré est plus long que le texte original car l'algorithme produit des résultats dont la longueur est un multiple de 16 octets (ou 128 bits).

Texte à chiffrer : Bonjour tous les amis!

On peut remarquer dans l'exemple que les caractères qui se répètent (les lettres o et s, et l'espace [· ] ) donnent un résultat différent à chaque fois.

On ne peut pas ainsi deviner que le o, par exemple, a été remplacé par le même caractère à chaque fois. On ne peut pas déterminer non plus qu'il a été déplacé ailleurs dans le texte.

Il n'est même pas possible de reconstituer le texte original en utilisant le seul texte chiffré par lui-même. Pour pouvoir le déchiffrer il faut avoir la clé. Une personne malintentionnée qui ne connaît pas la valeur de la clé devra tenter d'en deviner la valeur par différents moyens (mots de passe faibles, attaque par dictionnaire, attaque par force brute, etc.). Le principe d'avoir une clé commune dont la valeur est connue à la fois de l'émetteur et du destinataire (et personne d'autre!) fait en sorte que la clé est « symétrique » comme mentionné en début d'article.

La clé de chiffrement pour l'algorithme a une longueur de de 256 bits, ce qui est reflété dans la partie numérique du nom de l'algorithme.

2. Principes généraux de fonctionnement

2.1 Génération des clés de transformation

Avant de commencer le chiffrement, l'algorithme procède à la génération de 16 clés de transformation, d'une longueur de 128 bits chacune. Cette opération se fait pas paires de clés. Les deux premières clés sont mises à jour avec les valeurs des deux moitiés de la clé initiale de chiffrement, appelée ici K_init, qui est d'une longueur de 256 bits. Ensuite, chaque paire de clés propage des nouvelles valeurs à conserver dans la prochaine paire de clés.

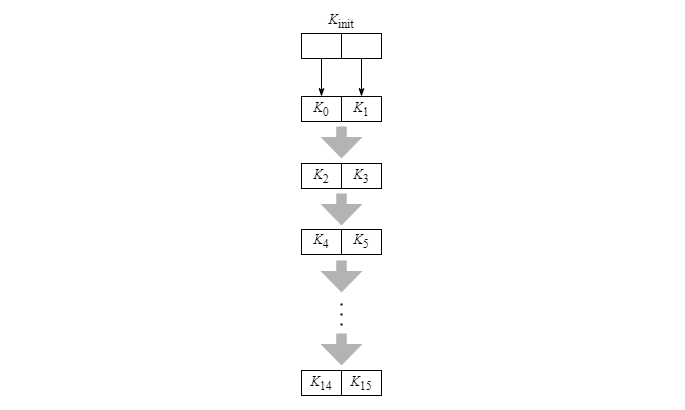
Le traitement utilisé pour déterminer les nouvelles valeurs de clés d'une paire à l'autre est passablement complexe. Pour les lecteurs qui veulent en savoir davantage, les détails à ce sujet sont présentés à l'annexe A (Détails sur la génération des clés de transformation).

2.2 Traitement par blocs de 128 bits ou 16 caractères

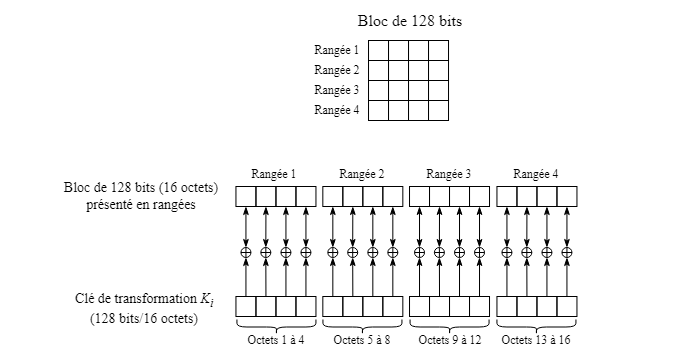
L'algorithme AES‑256 dans sa forme la plus simple consiste sommairement à séparer le texte brut, qui peut avoir une longueur quelconque, en blocs de 128 bits (16 caractères ou octets) disposés conceptuellement en 4 rangées et 4 colonnes, et à appliquer le chiffrement sur ceux-ci en employant les clés de transformation (la clé K₁₅ n'est pas utilisée).

2.3 Chiffrement d'un bloc de 128 bits

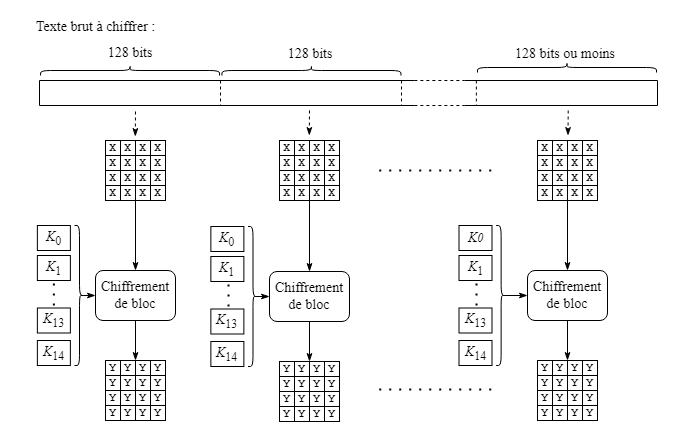
L'opération de chiffrement individuel sur un bloc de 128 bits commence par un OU exclusif entre ce bloc et la clé de transformation K₀ (dont la longueur est également de 128 bits). Par la suite, une application successive de 14 rondes de transformation est effectuée sur le bloc. Les rondes sont numérotées de 1 à 14 et chaque ronde utilise la clé de transformation avec le même numéro.

2.4 Ronde de transformation

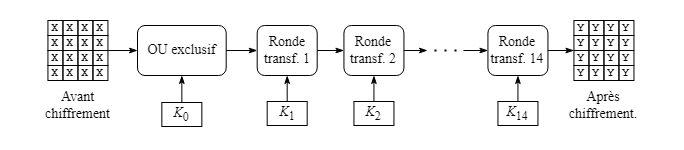
Dans une ronde de transformation, les opérations suivantes sont appliquées successivement au bloc de 128 bits :

• Substitution de caractères : la valeur chaque caractère du bloc est substituée par une valeur selon un tableau de correspondance prévu à cette fin;
• Décalage gauche rangée par rangée : les octets sont déplacés en restant toutefois dans leur rangée respective;
• Mélange des valeurs par colonne : la valeur de chaque octet est recalculée en fonction des valeurs des autres octets à l'intérieur de la même colonne. À noter que cette opération n'est pas effectuée lors de la dernière ronde de transformation, la ronde 14;
• OU exclusif : opération faite entre le bloc de 128 bits et la clé de transformation.

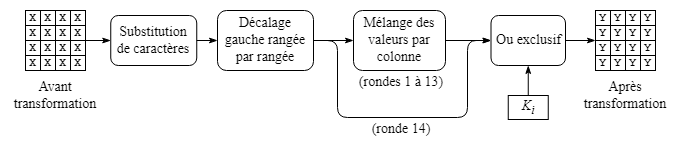
Pour les lecteurs qui veulent en savoir plus, une description plus approfondie des opérations effectuées lors d'une ronde de transformation est donnée à la section 4 (Détail des opérations d'une ronde de transformation d'un bloc).

2.5 Déchiffrement

Le déchiffrement fait par le destinataire d'un texte chiffré par un émetteur consiste à appliquer, sauf pour le OU exclusif, les mêmes opérations que celles employées pour le chiffrement, mais en utilisant un procédé inverse.

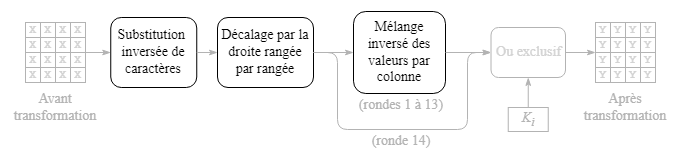
Pour que le déchiffrement puisse être mené à bien, le destinataire doit disposer de la même clé de chiffrement que l'émetteur afin de pouvoir générer les mêmes clés de transformation.

3. Modes d'utilisation de l'algorithme

L'algorithme AES-256 peut être utilisé selon plusieurs modes dont quelques-uns sont présentés dans cette section.

3.1 Mode ECB (Electronic Code Book)

Le mode ECB est essentiellement celui présenté en début de section précédente. Avec celui-ci, les blocs de 128 bits sont chiffrés indépendamment les uns les autres. Il s'agit du mode le plus simple mais aussi le plus vulnérable. En particulier, si deux blocs du texte brut ont le même contenu avant chiffrement, ceux-ci auront aussi le même contenu après chiffrement, une situation à éviter. En raison de ces désavantages, le mode ECB est très peu utilisé dans la pratique courante.

3.2 Mode CBC (Cipher Block Chaining)

Dans ce mode, le résultat du chiffrement du bloc 1 est utilisé en entrée au chiffrement du bloc 2 en le combinant au préalable par un OU exclusif au contenu du texte brut pour le bloc 2. Le même principe est appliqué pour passer du bloc 2 au bloc 3 et ainsi de suite. Un OU exclusif est également employé au départ pour chiffrer le bloc 1, en utilisant un « vecteur d'initialisation » (IV, de l'anglais Initialization Vector) qui est en fait un nombre aléatoire.

Le vecteur IV est de la même longueur qu'un bloc (128 bits) et est connu à la fois de l'émetteur et du destinataire. Le vecteur IV n'a pas besoin d'être secret. Le mode CBC offre plus de robustesse que le mode ECB mais est en revanche plus lent car il faut traiter séquentiellement les blocs, un désavantage que n'a pas le mode ECB, qui permet un traitement en parallèle des blocs.

3.3 Mode CTR (CounTeR)

Dans ce mode, le chiffrement ne se fait pas sur le texte brut lui-même mais sur la combinaison d'un nombre aléatoire avec un compteur; par la suite un OU exclusif du résultat du chiffrement est effectué avec le texte brut, bloc par bloc. Le compteur est incrémenté en passant d'un bloc à l'autre.

Le nombre aléatoire n'est pas secret mais doit être différent à chaque nouvelle transmission de message au cours d'une même session. Le nombre aléatoire et le compteur peuvent avoir une longueur quelconque mais le total des deux données jointes bout à bout ensemble (i.e. concaténation) devrait être de 128 bits.

Le mode CTR offre l'avantage de la robustesse tout en permettant le parallélisme. Même si le chiffrement porte sur une donnée qui varie peu d'un bloc à l'autre (i.e. incrémentation d'un compteur), cela n'a pas d'impact car le chiffrement avec l'algorithme AES-256 est conçu de manière à donner des résultats très différents, même entre deux données presque semblables.

3.4 Mode GCM (Galois Counter Mode)

Le mode GCM est une extension du mode CTR décrit à la section précédente, à laquelle est ajouté un traitement pour produire un code d'authentification de message MAC (de l'anglais Message Authentication Code) permettant de s'assurer de la bonne identité de l'émetteur et aussi de vérifier l'intégrité des données dans le cas où elles auraient été corrompues suite à une défaillance technique quelconque dans la communication. Le mode GCM fait partie de la classe avancée AE (pour Authenticated Encryption) pour l'algorithme AES-256.

Le mode GCM est plus complexe que les autres modes et fait appel à la théorie des corps finis développée par le mathématicien éponyme Évariste Galois au début du XIX^e siècle.

Le déroulement décrit de façon très sommaire pour le mode GCM est présenté dans les étapes qui suivent.

3.4 1 Chiffrement préparatoire en mode CTR

L'émetteur procède au chiffrement par blocs du texte secret en utilisant le mode CTR de la même manière que celle indiquée à la section précédente, avec un vecteur d'initialisation (IV) comme nombre aléatoire et un compteur. Dans la pratique courante, le vecteur IV est différent à chaque transmission de données, même à l'intérieur d'une même session entre l'émetteur et le récepteur, de manière à éviter de possibles répétitions de données qui pourraient donner des indices à des observateurs externes inopportuns.

La longueur de la combinaison du vecteur IV et du compteur doit être de 128 bits.

L'émetteur définit également des données additionnelles d'authentification (AAD, de l'anglais Additional Authenticated Data) de son choix (ex. : adresse IP) en préparation de la production du code MAC.

3.4 2 Production du code d'authentification de message (MAC)

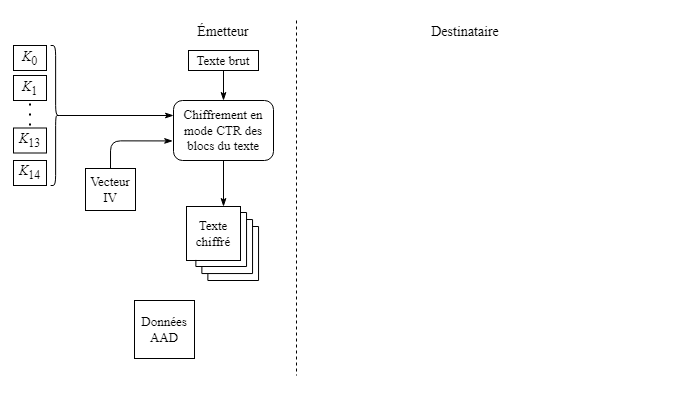
L'opération se déroule en trois parties. L'émetteur effectue d'abord un chiffrement dans un simple bloc de 128 bits du vecteur IV en appliquant les 15 rondes de transformation comme indiqué précédemment à la section 2.3.

L'émetteur procède ensuite à une opération particulière de multiplication entre les valeurs dans les blocs de 128 bits et celles contenues dans les données AAD. Sans trop entrer dans des détails qui peuvent être complexes, cette multiplication, basée sur la théorie des corps finis, permet d'avoir un résultat de 128 bits unique et quasi-aléatoire d'une fois à l'autre. Il est possible d'en savoir un peu plus concernant l'utilisation des corps finis pour l'algorithme AES‑256 en se référant à l'annexe B (Utilisation des corps finis avec l'algorithme).

Une fois la multiplication complétée, un OU exclusif est effectué avec le résultat de celle-ci et le vecteur IV chiffré dans un bloc de 128 bits. Le résultat de l'opération constitue le code MAC.

3.4 3 Envoi par l'émetteur/réception par le destinataire

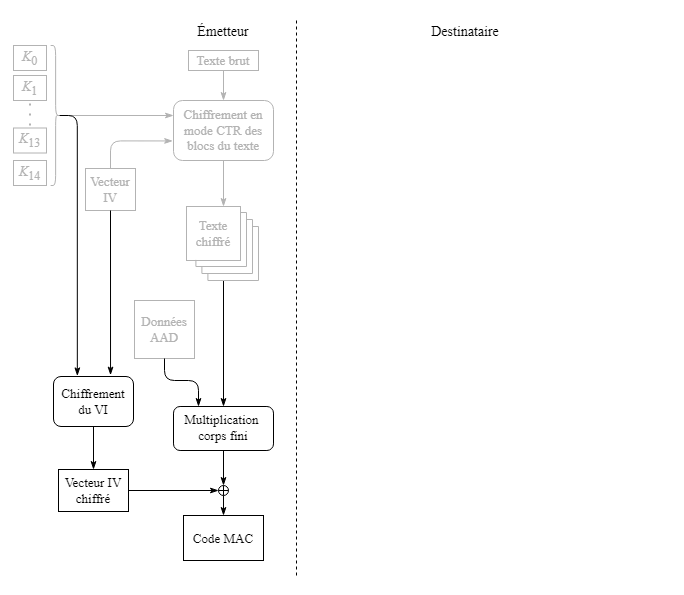
Lorsque l'émetteur a terminé sa tâche, l'émetteur envoie au destinataire les données qu'il a préparées : texte chiffré en blocs, le code MAC, le vecteur IV et les données AAD.

3.4 4 Déchiffrement du texte par le destinataire

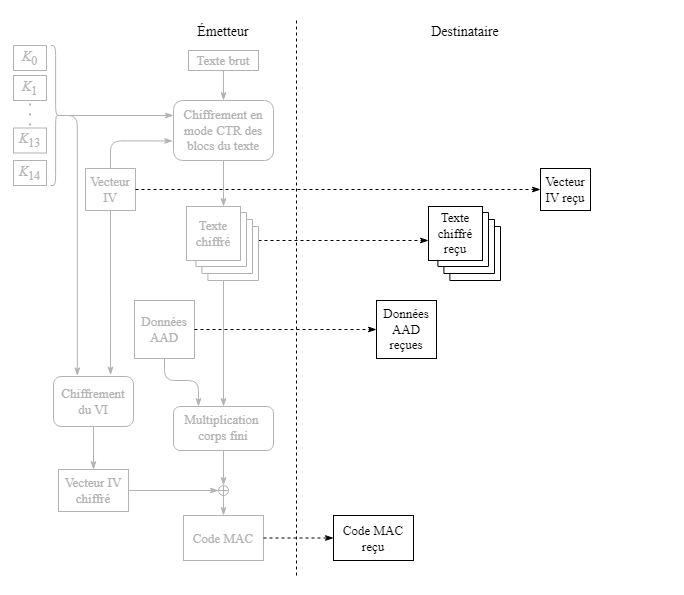
Le destinataire procède au déchiffrement du texte en utilisant le mode CTR, tel qu'expliqué plus tôt à la section 3.3, en employant le vecteur IV comme nombre aléatoire et un compteur comme l'a fait l'émetteur. Le déchiffrement est fait selon le procédé inverse du chiffrement tel que décrit à la section 2.5, pour chaque ronde de transformation et pour chaque bloc de 128 bits.

3.4 5 Production du code MAC par le destinataire

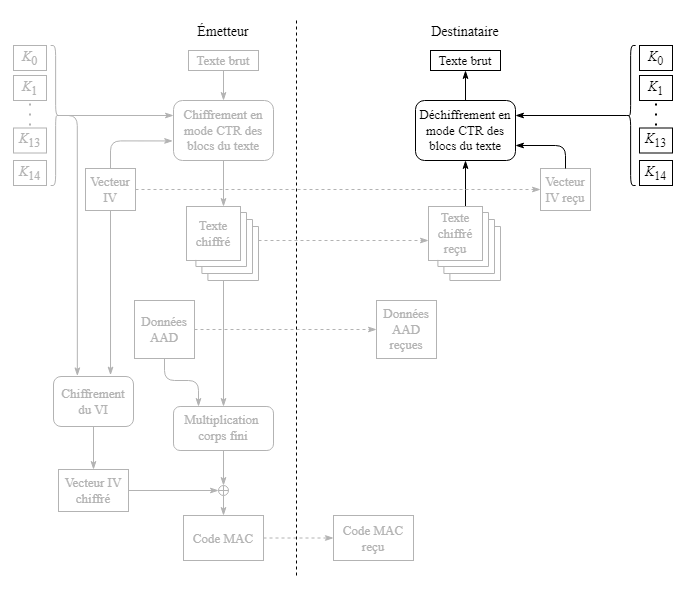
Après avoir déchiffré le texte, le destinataire produit le code MAC exactement de la même manière que l'émetteur : en chiffrant le vecteur IV reçu, en applicant la multiplication dans un corps fini des données AAD et du texte chiffré reçus, puis en faisant un OU exclusif entre le vecteur IV chiffré de 128 bits et le résultat sur 128 bits de la multiplication dans un corps fini.

3.4 6 Comparaison des codes MAC par le destinataire

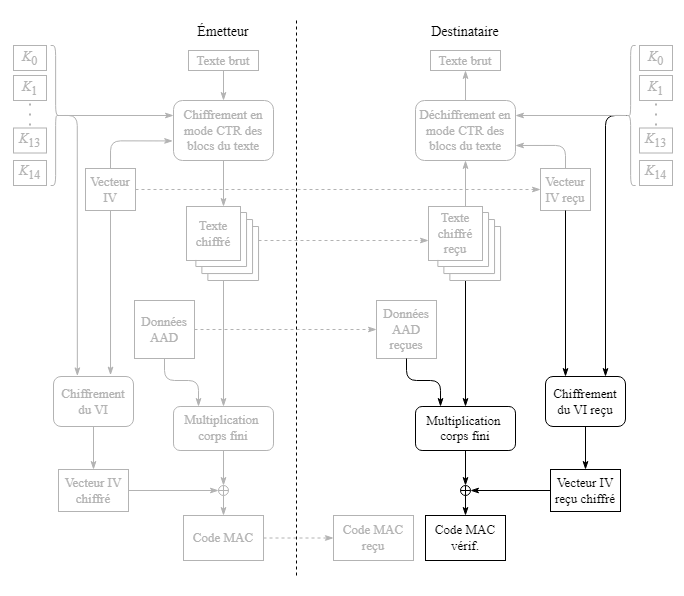
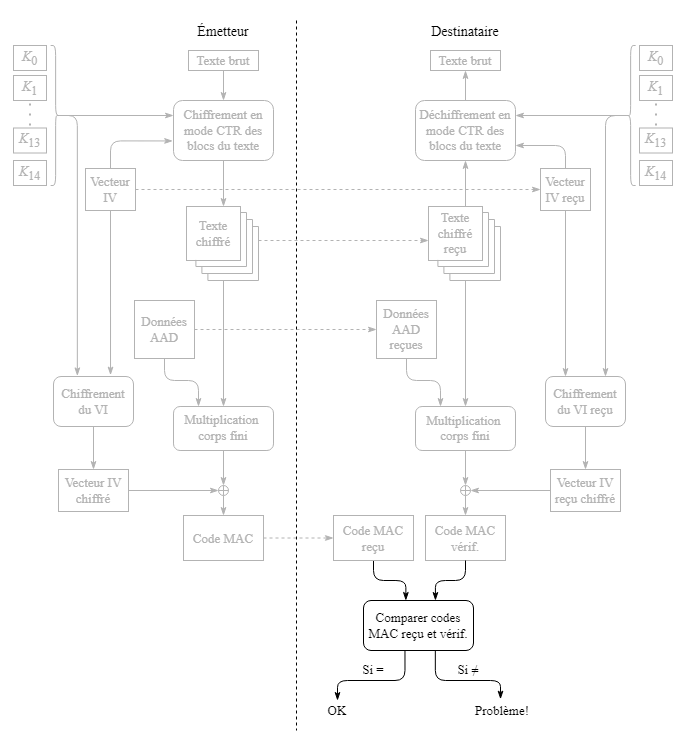
Le destinataire compare le code MAC de vérification qu'il vient de produire avec celui qu'il a reçu de l'émetteur. Si les deux codes sont identiques, l'identité de l'émetteur est confirmée.

Une différence entre les codes MAC indique que l'une ou l'autre des données reçues a été altérée soit par une défectuosité dans le lien entre l'émetteur et le destinataire, soit par une intervention malveillante. Dans tous les cas, le destinataire devrait mettre fin à la session.

4. Détail des opérations d'une ronde de transformation d'un bloc

La présente section donne une description détaillée des opérations effectuées lors d'une ronde de transformation d'un bloc de 128 bits présentées précédemment en aperçu de haut niveau à la section 2.4. Quelques connaissances concernant les matrices en mathématiques peuvent être utiles pour la compréhension de certaines parties de cette section.

À titre de rappel, une ronde de transformation de bloc est constituée des opérations suivantes :

• Substitution de caractères;
• Décalage gauche rangée par rangée;
• Mélange des valeurs par colonne;
• OU exclusif.

4.1 Substitution de caractères

Cette opération consiste à substituer chaque caractère du bloc par un caractère correspondant en utilisant à cette fin un tableau prédéfini, qu'on retrouve souvent sous le nom « S-box » (de l'anglais Substitution box) dans la documentation spécialisée au sujet d'AES-256.

Le tableau S-box est montré ci-dessous; les valeurs indiquées sont en notation hexadécimale. Les rangées correspondent aux 4 bits les plus significatifs du caractère à substituer et les colonnes correspondent aux 4 bits les moins significatifs du caractère. En suivant ce principe, on obtient bel et bien le caractère 6D comme caractère de substitution pour B3 dans le cas de l'exemple.

Il existe également un « tableau S-box inversé » contenant des valeurs différentes, non montré ici, pour faire la substitution en sens inverse lors du déchiffrement.

Dans certaines installations, le tableau S-box n'est pas implanté pour des raisons de sécurité. Dans un tel cas un traitement plus complexe, qui utilise la théorie ses corps finis, est effectué dynamiquement à chaque fois pour produire l'équivalent du tableau S-box pour un caractère donné. Plus de détails à ce sujet peuvent être obtenus à l'annexe C (Substitution de caractères sans tableau).

4.2 Décalage vers la gauche rangée par rangée

Pour cette opération, le décalage vers la gauche se fait de façon circulaire sur les rangées du bloc de 128 bits. Il n'y a pas de décalage pour la rangée 1 mais les autres rangées sont soumises à un décalage augmentant en nombre d'octets en passant d'une rangée à l'autre. Ainsi la rangée 2 est décalée de 1 octet, pour la rangée 3 le décalage est de 2 octets et pour la rangée 4, 3 octets.

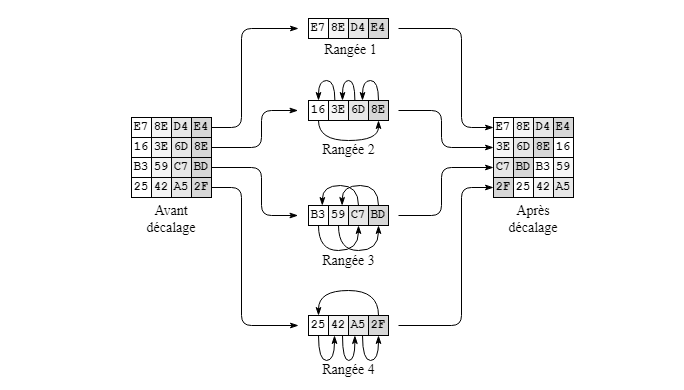
Pour le déchiffrement, l'opération se fait en sens inverse, vers la droite.

4.3 Mélange des valeurs par colonne

Cette opération, la plus complexe dans une ronde de transformation, consiste à appliquer pour chaque colonne du bloc de 128 bits un produit matriciel entre une matrice M de dimension 4 X 4, contenant les coefficients 02, 03, 01 et 01 déjà établis à l'avance par les concepteurs de l'algorithme, et la colonne (qui est de dimension 4 X 1).

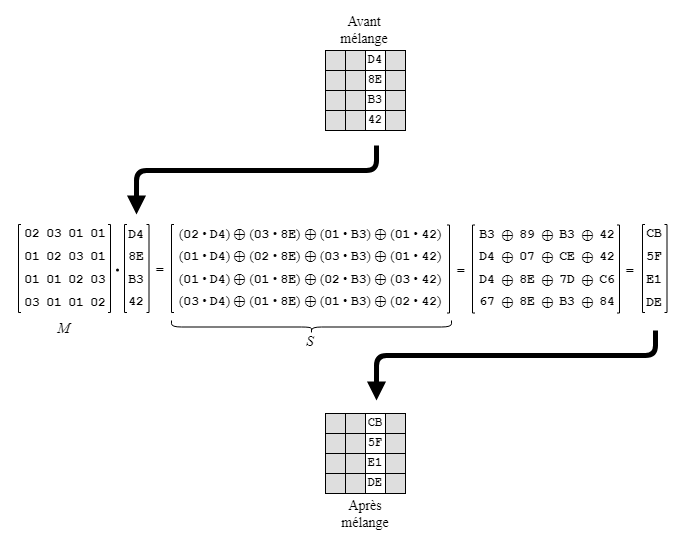
Les coefficients dans la matrice M se répètent d'une rangée à l'autre sauf que ceux-ci sont décalés d'une position vers la droite en changeant de rangée. Une matrice arrangée de cette sorte est dite « circulaire ».

Le développement terme à terme du produit matriciel, identifié par la partie S dans l'exemple ci-dessus, est décrit plus en détail à la prochaine section.

La multiplication à la base du produit matriciel employé pour le mélange des valeurs consiste en une multiplication dans un corps fini dont plus de détails sont donnés plus loin à la section 4.3.2.

4.3 1 Développement terme à terme du produit matriciel

Comme nous venons de voir dans l'exemple montré plus haut, le contenu de la partie S représentant le développement terme à terme du produit matriciel est passablement complexe.

Plutôt que de se référer au formalisme de l'algèbre matricielle avec laquelle il pourrait être facile de s'y perdre pour voir comment on arrive à la partie S, utilisons une astuce visuelle. Celle-ci consiste à déterminer le contenu de la partie S, qu'on peut conceptualiser comme une « surface de travail », à partir de la matrice M de dimension 4 X 4 et de la colonne C de dimension 4 X 1. Les étapes de la « recette » sont présentées ci-dessous.

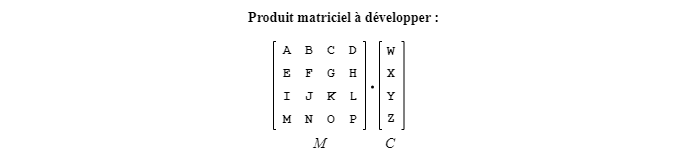
1. Faire pivoter de 90° dans le sens anti-horaire la colonne C de manière à avoir un en-tête pour la surface de travail. Déplacer vers la droite le crochet droit de C de manière à délimiter la surface de travail :

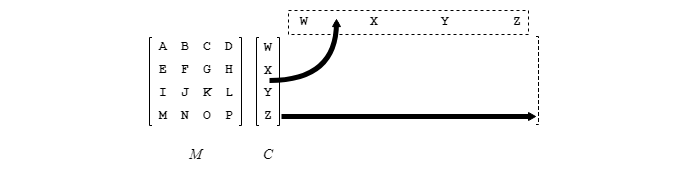
2. Reproduire le contenu complet de M dans S :

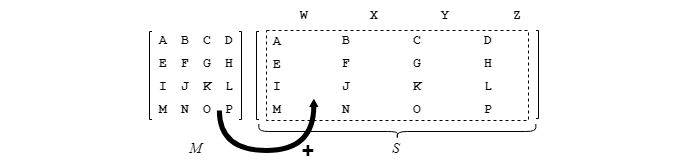
3. Dupliquer dans les colonnes correspondantes de S les valeurs provenant initialement de C mises en en-tête :

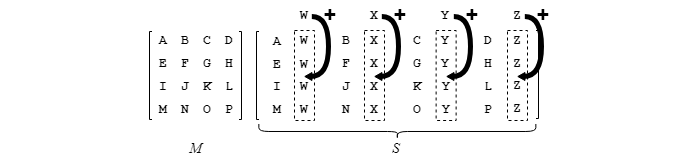
4. Insérer les opérateurs dans S!

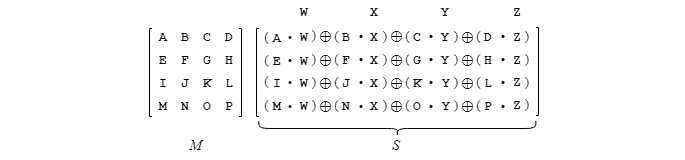
À ce point-ci le développement terme à terme est complété et prêt au calcul des résultats. Reprenons le procédé avec l'exemple de la figure 16 montré plus haut.

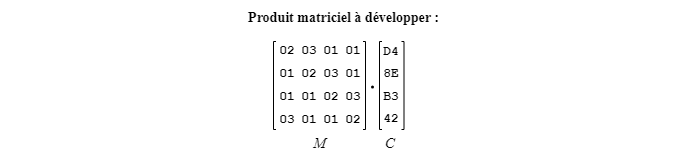
1. Faire pivoter la colonne C.

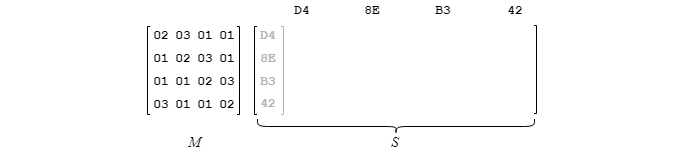
2. Reproduire le contenu complet de M dans S.

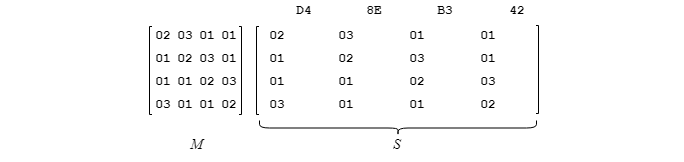
3. Dupliquer dans les colonnes correspondantes les valeurs provenant initialement de C mises en en-tête.

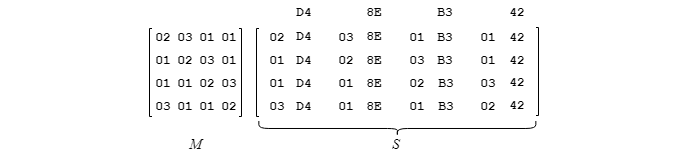
4. Insérer les opérateurs.

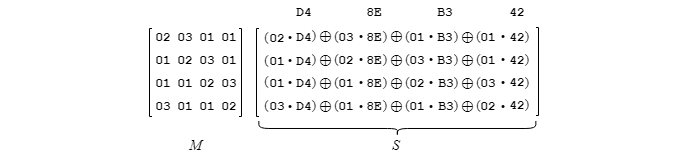
En appliquant ensuite la multiplication pour chaque paire des termes, puis en additionnant (par un OU exclusif) ces résultats intermédiaires rangée par rangée, on obtient le résultat final de la multiplication pour une colonne.

4.3 2 Multiplication dans un corps fini

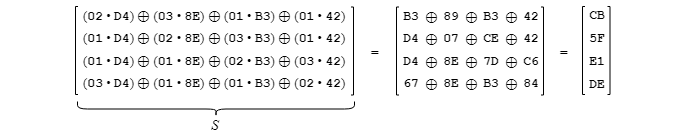
La multiplication dans un corps fini pour le mélange des valeurs dans une colonne doit être appliquée entre chaque cellule de la matrice de coefficients et chaque octet de la colonne. Il s'agit d'une opération fort complexe qui peut toutefois être contournée en utilisant des tableaux de multiplication déjà existants prévus à cette fin. Certains détails concernant l'utilisation des corps finis pour l'algorithme AES‑256 sont donnés dans l'annexe B (Utilisation des corps finis avec l'algorithme).

Pour les paires avec le multiplicande 01, aucun tableau n'est nécessaire car le résultat est le même que le multiplicateur. Par exemple pour la paire (01· B3), le résultat est B3.

Si on veut faire le calcul pour la paire (02· 8E) de l'exemple, on utilise le tableau montré un peu plus bas pour la valeur 02.

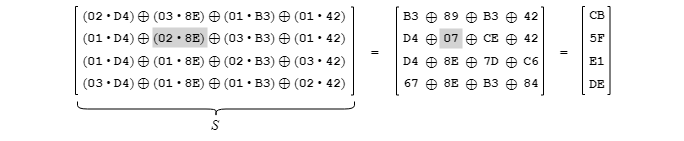
Dans le tableau, les rangées correspondent aux 4 bits les plus significatifs du multiplicateur 8E et les colonnes correspondent à ses 4 bits les moins significatifs, ce qui permet d'obtenir le résultat 07 pour (02· 8E).

Et si on veut faire le calcul pour la paire (03· D4) de l'exemple, on utilise le tableau pour la valeur 03, montrée un peu plus bas.

En accédant à la rangée correspondant aux 4 bits les plus significatifs du multiplicateur D4 et la colonne correspondant à ses 4 bits les moins significatifs, on obtient le résultat 67 pour (03· D4).

4.3 3 Déchiffrement

Le déchiffrement s'effectue de la même manière qu'avec le chiffrement mais en utilisant un matrice M contenant des coefficients différents : 14, 11, 13 et 09. Le contenu de la matrice est présenté ci-dessous et il existe aussi des tableaux de multiplication pour ces coefficients.

4.4 OU exclusif

Contrairement à l'opération de mélange des valeurs par colonne vue dans la section précédente, l'opération du OU exclusif est beaucoup moins complexe.

Celle-ci consiste à effectuer un OU exclusif entre le bloc de 128 bits et la clé de transformation K_i, également d'une longueur de 128 bits, pour la ronde de transformation en cours. Le résultat est remis dans le bloc de 128 bits.

Cette opération s'applique aussi avec la clé K₀ du début du chiffrement d'un bloc de 1024 bits avant d'effectuer les rondes de transformation comme déjà mentionné à la section 2.3.

5. Volet sécurité

5.1 Famille d'algorithmes AES

La famille d'algorithmes AES dont AES-256 fait partie inclut les algorithmes AES-128 et AES-192, qui utilisent des clés de 128 bits et 192 bits respectivement. En comparaison avec ceux-ci, AES-256 offre un meilleure sécurité en raison de la longueur de sa clé qui permet d'avoir 2²⁵⁶ valeurs possibles (de l'ordre de 10⁷⁷).

En contrepartie, AES-256 est moins rapide que les autres variantes de la famille AES parce que ces derniers effectuent moins de rondes de transformation par bloc de 128 bits : 10 pour AES-128, 12 pour AES-192, comparativement à 14 pour AES-256.

Dans la pratique courante, les algorithmes AES-128 et AES-256 sont les plus utilisés sur Internet, et ce, à peu près à parts égales. Pour les contextes où la rapidité est privilégiée (ex. : applications mobiles), AES-128 est le choix qui s'impose. Les secteurs pour lesquels des données sensibles peuvent être utilisées (ex. : gouvernement, armée, finance) vont adopter de leur côté AES-256. L'utilisation de AES-192, de son côté, est relativement marginale.

Le tableau ci-dessous donne la liste des algorithmes de la famille AES et les différences entre eux.

5.2 Clé symétrique

La clé symétrique à utiliser pour les algorithmes de la famille AES doit être connue à la fois de l'émetteur et du destinataire. Pour que les deux parties aient au départ la même valeur de cette clé, cela ne se fait pas par une décision de l'une de celles-ci qui transmet ensuite la valeur de la clé à l'autre, ce qui créerait un risque d'interception de la clé.

Heureusement, la plupart des protocoles modernes de communication (TLS, Signal, Wireguard, etc.) comportent un mécanisme permettant à chacune des deux parties de calculer séparément la valeur de la clé et d'arriver au même résultat sans jamais à faire transiter celui-ci.

5.3 Perspectives d'avenir

Bien que les ordinateurs augmentent continuellement en puissance, ils seront toujours trop lents pour effectuer une attaque par force brute visant à déterminer la valeur d'une clé utilisée par les algorithmes de la famille AES. Ces algorithmes de chiffrement offrent actuellement un haut niveau de confiance pour la sécurisation des données.

L'émergence des ordinateurs quantiques actuellement en progression peut toutefois changer la donne. L'algorithme de Grover conçu pour ce type d'appareils permettrait de réduire de la racine carrée l'effort requis pour une attaque par force brute.

Pour l'algorithme AES-256, cela ramenerait à un nombre de l'ordre de 10³⁸ possibilités à tester pour une attaque, un effort qui n'est toujours pas envisageable pour que l'attaque puisse être effectuée dans un délai réalisable, même pour un ordinateur quantique. Les perspectives d'avenir pour l'algorithme AES-256 restent bonnes car l'ordre de complexité requis par l'algorithme de Grover pour tenter de le fragiliser demeure exponentiel.

AES-128 est plus vulnérable face aux ordinateurs quantiques en raison de sa clé plus courte qui ferait en sorte qu'une attaque par force brute avec l'algorithme de Grover nécessiterait un effort de 2⁶⁴ (environ 10¹⁹) opérations, un chiffre qui devient plausible. Un passage à AES-256 permettrait à coût réduit d'écarter les risques d'une attaque par force brute.

La menace posée par les ordinateurs quantiques vise davantage les algorithmes à clé publique, comme RSA et Diffie-Hellman, qui viennent en support à ceux de la famille AES. Pour ce type d'algorithmes, l'effort requis avec un ordinateur quantique pour les déjouer serait réduit à un ordre non exponentiel en utilisant un algorithme dédié à cette tâche, l'algorithme de Shor. Cette possibilité constitue une menace plus sérieuse. L'algorithme de Shor est conçu spéfiquement pour les algorithmes à clé publique et ne peut pas s'appliquer aux algorithmes de la famille AES.

C'est surtout pour contrer l'algorithme de Shor que des efforts sont actuellement consacrés à une transition vers des algorithmes dits « post-quantiques », comme Kyber et Dilithium, en remplacement des algorithmes à clé publique existants. Le tableau ci-dessous montre un récapitulatif concernant le passage à l'éventuelle ère quantique des algorithmes actuels.

Bien que pour le futur l'algorithme AES-256 paraît mieux blindé contre les ordinateurs quantiques que les autres algorithmes, des algorithmes plus performants que Grover pourraient voir le jour et compromettre sa sécurité. Dans cette optique, la recherche d'alternatives post-quantiques pour en prendre éventuellement la relève est de mise.

6. Conclusion

Par l'utilisation d'une clé de chiffrement initiale qui fait propager des valeurs différentes à un ensemble de clés de transformation, l'algorithme AES-256, tout comme les autres algorithmes de la famille AES, permet le chiffrement d'un texte secret et la transmission de celui-ci à un destinataire sans qu'un observateur indiscret durant la communication puisse déterminer le contenu du texte brut initial.

Le destinataire, qui connaît la valeur de la clé de chiffrement au même titre que l'émetteur, peut déchiffrer le texte secret en utilisant cette clé.

Le chiffrement et le déchiffrement du texte se font par blocs de 128 bits. Pour chaque bloc, une série de 10, 12 ou 14 rondes de transformation, selon l'algorithme AES utilisé, est effectuée en utilisant les clés de transformation générées à partir de la clé initiale de chiffrement.

Chaque ronde de transformation de bloc est constituée des opérations suivantes :

• Substitution de caractères;
• Décalage gauche rangée par rangée;
• Mélange des valeurs par colonne;
• OU exclusif.

Tous les algorithmes de la famille AES peuvent être appliqués selon plusieurs modes comme ECB, CBC, CTR et GCM. Le mode GCM est actuellement la norme dans les échanges sur Internet car celui-ci permet d'authentifier l'identité de l'émetteur, ce qui n'est pas possible avec les autres modes.

Références

Pages Wikipédia

Utilitaire de test

Annexe A - Détails sur la génération des clés de transformation

Comme il a été mentionné précédemment à la section 2.1, la génération des clés de transformation K₀ à K₁₅, d'une longueur de 128 bits chacune, se fait par paires de clés et les deux premières clés K₀ et K₁ sont mises à jour avec les valeurs des deux moitiés de la clé initiale de chiffrement de 256 bits.

Chaque paire de clés propage ensuite des nouvelles valeurs à conserver dans la prochaine paire de clés par un procédé complexe dont les détails sont donnés dans cette annexe. Conceptuellement, chaque paire de clés commence par une clé de rang pair (ex. : K₈) et finit forcément par une clé de rang impair (ex. : K₉).

Pour la propagation des valeurs de clés, chaque clé (de 128 bits) dans une paire de clés est conceptuellement divisée en 4 « mots » de 32 bits. Le premier mot d'une clé de rang pair, et par le fait même d'une paire de clés, fait l'objet d'un traitement particulier alors que les autres mots dans la paire de clés sont soumis à un traitement plus régulier.

Prendre note que les détails présentés dans cette annexe ne s'appliquent qu'à l'algorithme AES-256. Le traitement pour les autres algorithmes AES-128 et AES-192 de la famille AES est similaire mais comporte tout de même certaines différences en raison des longueurs de clés et des nombres de rondes qui ne sont pas les mêmes.

A.1 Premier mot de 32 bits d'une clé rang pair

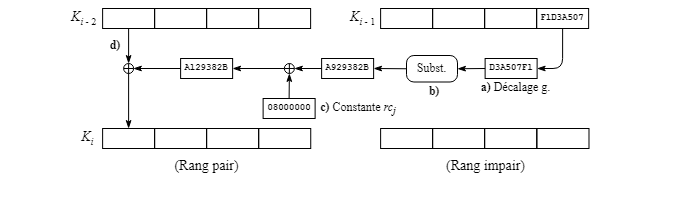
Pour le cas particulier du premier mot de 32 bits d'une clé rang pair, les opérations suivantes sont effectuées à partir des deux clés K_{i - 2} et K_{i - 1} qui précèdent celle de rang pair K_i dont on veut mettre à jour le premier mot :

1. Décalage circulaire d'un octet vers la gauche appliqué sur une copie du dernier mot de 32 bits de la clé de rang impair K_{i - 1} qui précède;
2. Substitution de chacun des 4 caractères (de 8 bits) selon la méthode montrée précédemment à la section 4.1;
3. OU exclusif du résultat précédent avec la constante d'expansion rc_j appropriée correspondant à la ronde i. Les différentes valeurs de cette constante sont montrées dans la liste ci-dessous (à titre d'exemple dans la figure plus haut, rc₄ = 08000000 est utilisée, ce qui fait que i correspond à 8) :
   • rc₁, associée à K₂; valeur : 01000000;
   • rc₂, associée à K₄; valeur : 02000000;
   • rc₃, associée à K₆; valeur : 04000000;
   • rc₄, associée à K₈; valeur : 08000000;
   • rc₅, associée à K₁₀; valeur : 10000000;
   • rc₆, associée à K₁₂; valeur : 20000000;
   • rc₇, associée à K₁₄; valeur : 40000000.
4. Encore un OU exclusif entre le résultat précédent et le premier mot de 32 bits de la clé de rang pair K_{i - 2} qui précède.

Le résultat de la dernière étape est alors mis dans le premier mot de la clé de rang pair K_i qu'on est en train de traiter.

A.2 Traitement des autres mots de 32 bits d'une paire de clés

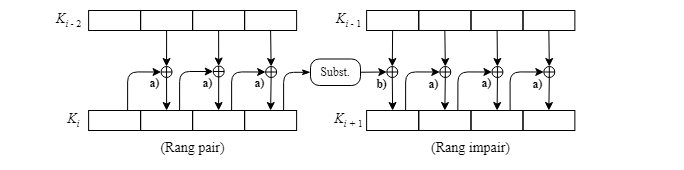
Les opérations ci-dessous sont effectuées pour chacun des mots après le premier mot pour la paire de clés K_i et K_{i + 1}, en utilisant la paire de clés K_{i - 2} et K_{i - 1} qui précèdent :

1. OU exclusif entre le mot de 32 bits qui précède immédiatement et le mot à la même position dans la paire de clés qui précède;
2. S'il s'agit du premier mot de la clé de rang impair K_{i + 1}, OU exclusif entre la substitution de chacun des 4 caractères appliquée (selon la méthode de la section 4.1) au dernier mot de la clé de rang pair K_i qui précède et le premier mot de la clé de rang impair K_{i - 1} qui précède.

Annexe B - Utilisation des corps finis avec l'algorithme

L'utilisation des corps finis constitue un élément fondamental dans le principe de fonctionnement de l'algorithme AES-256. En particulier, l'opération de « multiplication dans un corps fini », mentionné à certaines reprises dans l'article, s'avère très utile en raison de son potentiel pour produire des résultats de façon quasi-aléatoire.

B.1 Quelques notions de base

Sans entrer dans le détail de la théorie des corps finis pour ne pas déborder du cadre de l'article, nous allons nous référer aux corps finis qui concernent directement l'algorithme AES-256 selon la notation employée dans la théorie : F₂₅₆ et F₂128. Bien qu'un corps fini soit souvent représenté par des polynômes, il peut aussi l'être par des nombres binaires lorsque celui-ci s'applique à une puissance de 2, ce qui est le cas pour AES-256.

Pour effectuer une opération dans un corps fini (multiplication, inverse multiplicatif), un polynôme dit « irréductible » doit être utilisé à cette fin. Celui-ci permet de s'assurer que le résultat de l'opération reste dans le corps fini.

B.2 Corps fini F₂₅₆

Pour l'algorithme AES-256, le corps fini F₂₅₆ est utilisé pour les opérations suivantes :

• Substitution de caractères sans tableau (inverse multiplicatif dans un corps fini);
• Mélange des valeurs par colonne (multiplication dans un corps fini).

Comme il a été vu dans les sections correspondant à ces opérations, des tableaux peuvent être utilisés directement sans utiliser les corps finis mais le recours à ceux-ci demeure facultatif. Certaines organisations peuvent décider de plutôt effectuer dynamiquement à chaque fois les opérations s'appliquant au corps fini F₂₅₆ permettant d'avoir l'équivalent de ce qui peut être obtenu à partir des tableaux.

Le polynôme irréductible utilisé pour les opérations dans le corps fini F₂₅₆ pour l'algorithme AES-256 est le suivant (en binaire, les positions de bits à 1 correspondent aux puissances de x présentes dans le polynôme) :

Un exemple détaillé de multiplication dans le corps fini F₂₅₆ peut être consulté dans l'article Corps finis et chiffrement des données.

B.3 Corps fini F₂128

Pour l'algorithme AES-256, le corps fini F₂128 est utilisé pour l'opération suivante :

• Production du code d'authentification de message (MAC) pour le mode GCM (multiplication dans un corps fini).

Le polynôme irréductible utilisé pour une opération dans le corps fini F₂128 pour l'algorithme AES-256 est le suivant :

x¹²⁸ + x⁷ + x² + x + 1 (hexadécimal : 1 00000000 00000000 00000000 00000087)

Le corps fini donne accès à 2¹²⁸ valeurs possibles (de l'ordre de 10³⁸ valeurs). Un tel chiffre exclut l'emploi de tableaux déjà définis à l'avance comme c'est le cas pour le corps F₂₅₆ et impose de lui-même l'utilisation dynamique des opérations dans le corps fini F₂128.

Annexe C - Substitution de caractères sans tableau

C.1 Utilisation de l'inverse multiplicatif

La construction du tableau S-box utilisé pour la substitution de caractères repose, du moins en partie, sur l'opération d'inverse multiplicatif dans le corps fini F₂₅₆ de la valeur du caractère à substituer, comme mentionné à l'annexe précédente.

Le calcul de l'inverse multiplicatif dans un corps fini peut être fait de plusieurs manières pour un nombre donné du corps fini, notamment en l'élevant à la puissance 254 pour le corps fini F₂₅₆. Cela peut être fait en seulement quelques étapes de multiplication du nombre par lui-même dans le corps fini en utilisant un polynôme irréductible. La méthode employée est décrite plus en détail dans l'article Corps finis et chiffrement des données

Pour la substitution de caractères, l'inverse multiplicatif doit être utilisé avec le même polynôme irréductible que celui mentionné à l'annexe précédente (x⁸ + x⁴ + x³ + x + 1 ou 100011011 [binaire] ou 11B [hexadécimal]). Plusieurs autres étapes, dites de « transformation affine », qui différent selon la partie où l'on applique l'algorithme AES-256 (chiffrement ou déchiffrement), sont aussi utilisées pour la substitution de caractères.

C.2 Substitution lors du chiffrement

La liste complète des étapes lors du chiffrement est donnée ci-dessous (C : caractère à substituer; S : caractère de substitution; I : inverse multiplicatif).

• Déterminer l'inverse multiplicatif I de C;
• S = I;
• S = OU exclusif de S avec valeur de I décalée de façon circulaire de 1 bit à gauche;
• S = OU exclusif de S avec valeur de I décalée de façon circulaire de 2 bits à gauche;
• S = OU exclusif de S avec valeur de I décalée de façon circulaire de 3 bits à gauche;
• S = OU exclusif de S avec valeur de I décalée de façon circulaire de 4 bits à gauche;
• S = OU exclusif de S avec valeur constante binaire 01100011 (63 en hexadécimal).

Si on prend l'exemple de C = D4 (hexadécimal), on peut déterminer que son inverse multiplicatif est C5 (voir le tableau des inverses multiplicatifs à la fin de l'article). Sans détailler toutes les étapes ci-dessus, on obtiendra 48 comme résultat.

C.3 Substitution inversée lors du déchiffrement

Pour avoir la valeur initiale C du caractère substitué à partir de celle du caractère de substitution S, les étapes ci-dessous, qui constituent l'inverse de la transformation montrée précédemment, doivent être effectuée lors du déchiffrement (T : variable de travail).

• T = 0000 0000;
• T = OU exclusif de T avec valeur de S décalée de façon circulaire de 1 bit à gauche;
• T = OU exclusif de T avec valeur de S décalée de façon circulaire de 3 bits à gauche;
• T = OU exclusif de T avec valeur de S décalée de façon circulaire de 6 bits à gauche;
• T = OU exclusif de T avec valeur constante binaire 0000 0101 (05 en hexadécimal);
• Déterminer l'inverse multiplicatif de T, ce qui donne directement la valeur voulue du caractère C.

Si on reprend le résultat du chiffrement précédent avec S = 48 (hexadécimal), on a la valeur C5 comme dernier résultat intermédiaire en appliquant les étapes ci-dessus, sans les détailler, avant de déterminer l'inverse multiplicatif de T . Et l'inverse multiplicatif de C5 est bel et bien D4, le caractère initial avant chiffrement.

C.4 Tableau des inverses multiplicatifs

Le tableau ci-dessous montre les inverses multiplicatifs dans F₂₅₆ avec le polynôme irréductible x⁸ + x⁴ + x³ + x + 1 (ou 100011011 [binaire] ou 11B [hexadécimal]) utilisé pour AES-256.

Ce tableau n'est utilisé ici que pour les fins de la présente démonstration et n'est pas implanté dans la pratique courante. Pour les installations qui utiliseraient l'inverse multiplicatif pour éviter d'utiliser le tableau S-box pour des raisons de sécurité, il n'y aurait aucun intérêt à employer un tableau des inverses multiplicatifs car celui-ci serait exposé aux mêmes risques que le tableau S-box. Pour de telles configurations, le calcul de l'inverse multiplicatif se fait dynamiquement.

Dans le tableau, les rangées correspondent aux 4 bits les plus significatifs du nombre dont on veut déterminer l'inverse multiplicatif et les colonnes correspondent à ses 4 bits les moins significatifs.